2. Інтерполяція за схемою Ейткена
Ітераційні методи інтерполяції засновані на повторному застосуванні деякою простий інтерполяційної схеми. Найбільш відомим з ітераційних методів є метод Ейткена, в основі якого лежить багаторазове застосування лінійної інтерполяції.
У відповідності зі схемою Ейткена лінійна інтерполяція по точкам Mi (xi. Yi) і Mi + 1 (xi + 1. Yi + 1) зводиться до обчислення визначника другого порядку
При інтерполяції по трьом і більше точкам послідовно обчислюються многочлени
У загальному випадку інтерполяційний многочлен n-го ступеня, який приймає в точках xi значення yi (i =), записуються в такий спосіб:
Основною перевагою схеми Ейткена є можливість поступового збільшення числа використовуваних значень xi до тих пір, поки послідовні значення P0,1,2, ..., n (x) і P1,2, ..., n-1 (x) не співпадуть в межах заданої точності . Інакше кажучи, обчислення припиняються при виконанні умови
При використанні ЕОМ обчислення за формулою (3) реалізуються у вигляді рекурсивної підпрограми - функції РХ (I, J) з формальними параметрами I, J, що визначають індекси крайніх вузлів інтерполяції, які використовуються для отримання значення відповідного многочлена Pi, i + 1, ..., j (x).
Для зберігання обчислених значень P (x) використовується двовимірний масив M розміром N * N елементів, де N - максимальне число вузлів інтерполяції. Кожному можливого значення P (x) відповідає один з елементів M (I, J), розташований вище головної діагоналі (I Наприклад, значенням многочлена P1,2 (x) відповідає елемент M (1,2), значенням P2,3,4 (x) - елемент M (2, 4) і т.д. Симетричні елементи M (J, I), розташовані нижче головної діагоналі (J> I), показують, обчислені відповідні значення P (x) на даний момент, і визначаються як Схема рекурсивної процедури PX приведена на рис. 1, де Х - масив значень вузлів інтерполяції, Y - масив значень функції у вузлах інтерполяції, Z - значення аргументу. Параметри X, Y, Z, M повинні бути описані як загальні для головної програми та підпрограми PX. 3. Інтерполяційні формули Ньютона для рівновіддалених вузлів Вузли інтерполяції x0. x1. xn називаються рівновіддаленими, якщо, де h - крок інтерполяції. При цьому для деякої функції f (x) таблично задаються значення yi = f (xi), де xi = x0 + ih.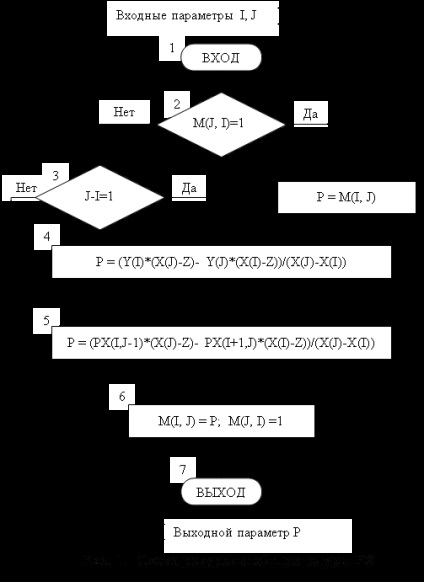
Існують дві формули Ньютона для випадку рівновіддалених вузлів інтерполяції, які називаються відповідно першої та другої інтерполяційними формулами Ньютона і мають вигляд:
;
,
У цих формулах D i yj - кінцеві різниці, де i - порядок різниці, j - її порядковий номер, а параметри t і q визначаються наступним чином:
Кінцеві різниці першого порядку обчислюються як Dyj = yj + 1 - yj. де
j =, для більш високих порядків використовується відома формула
Отримувані кінцеві різниці зручно представляти в табличній формі запису, наприклад, у вигляді табл. 1, яка називається горизонтальною таблицею кінцевих різниць.
Пepвая формула Ньютона застосовується для інтерполяції вперед і екстраполірованія тому, тобто на початку таблиці різниць, де рядки заповнені і є достатня кількість кінцевих різниць. При використанні цієї формули для інтерполяції значення аргументу x має лежати в інтервалі [x0. x1]. При цьому за x0 може прийматися будь-який вузол інтерполяції xk з індексом, де m - максимальний порядок кінцевих різниць.
Друга формула Ньютона застосовується для інтерполяції назад і екстраполірованія вперед, тобто в кінці таблиці кінцевих різниць. При цьому значення аргументу x має перебувати в інтервалі [xn-1. xn], причому за xn може прийматися будь-який вузол інтерполяції.
Одне з найважливіших властивостей кінцевих різниць полягає в наступному. Якщо кінцеві різниці i-го порядку (i де L - число значущих цифр після коми в поданні значень функції. Необхідно відзначити, що формули Ньютона є видозмінами формули Лагранжа. Однак у формулі Лагранжа можна нехтувати жодним з доданків, так як всі вони рівноправні і представляють многочлени n-го ступеня. У формули Ньютона як доданків входять многочлени підвищуються ступенів, коефіцієнтами при яких служать кінцеві різниці, розділені на факторіали. Кінцеві різниці, як правило, швидко зменшуються, що дозволяє в формулах Ньютона знехтувати складовими, коефіцієнти при яких стають малими. Це забезпечує обчислення проміжних значень функції досить точно за допомогою простих інтерполяційних формул. Інформація про роботу «Інтерполяція функцій»