Інтерполяційні квадратурні формули
Глава3. чисельне інтегрування
При чисельному диференціюванні доводиться віднімати один з одного близькі значення функції. Це призводить до знищення перших значущих цифр, тобто до втрати частини достовірних знаків числа.
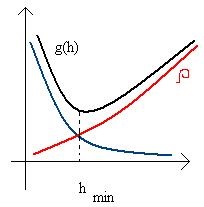
# 961; визначає похибка методу і необмежено убуває при h → 0. Але є і непереборна похибка, пов'язана з похибкою при обчисленні функції f (x):. Вона необмежено зростає при h → 0.
Таким чином, повна похибка не перевищує. А значить, оптимальним буде крок методу, відповідний мінімуму g (h).
Менший крок невигідний, а менша похибка недостіхіма. Ця мінімальна помилка тим менше, чим менше похибка вхідних даних.
Завдання полягає в наближеному обчисленні інтеграла. наприклад, по дискретним значенням функції f (x) у вузлах x1. xn. по заміні функції її апроксимацією і т.д.
Так - інтегральна сума. Загальний вигляд апроксимуючих сум. де Ak - деякі коефіцієнти.
Нехай потрібно знайти певний інтеграл,
де f (x) - дискретна функція, задана в вузлах x1 ... xn;
q (x)> 0 - вагова функція.
Тоді наближена формула обчислення має вигляд:
Права частина формули (1) - квадратура.
Може бути застосований наступний підхід: функція f (x) апроксимується інтерполяційним поліномом Pn-1 (x) по вузлах x1 ... xn.
Отримаємо для цього випадку формулу (1) і квадратуру шуканого інтеграла.
Передбачається, що . Отримаємо:.
- інтерполяційний поліном в Лагранжа,
Підставами в (1) замість функції f (x) поліном Pn-1 (x), отримаємо:
Похибка в цьому випадку бути подана у вигляді:.
За побудовою інтерполяціонная квадратурная формула точна,
Теорема 1 Квадратурна формула (1) точна для будь-якого многочлена Pk (x),
k ≤ n-1 тоді і тільки тоді, коли вона - інтерполяціонная.
Нехай формула (1) точна для будь-якого многочлена Pk (x), k ≤ n-1, тобто
Доведемо, що тоді Ak знаходяться за формулою (2).
Розглянемо функції - многочлени (n-1) ступеня:
Тоді виконується рівність:, тобто Ai обчислюються за формулою (2).
Нехай формула (1) інтерполяціонная, тобто Ak обчислюються по (2). Доведемо, що тоді (1) точна для будь-якого многочлена Pk (x), k ≤ n-1.
Розглянемо довільний многочлен Pk (x), k = n-1.
Його уявлення в формі Лагранжа має вигляд:
З іншого боку, його квадратура
, де Ak обчислюються за формулою (2), тобто I = J.
Що й потрібно було довести.
Оцінимо похибка квадратурної формули інтерполяційного типу: