Перш ніж перейти до формування та управління портфелем облігацій, необхідно розкрити основні фактори, що впливають на коливання цін облігацій.
Поточна ринкова ціна P 0 облігації, що має купонних виплат на рік, визначається за формулою:
де i / m величина прибутковості до погашення; Ct / m купонні виплати; Mmn номінал; n число років до погашення облігації.
Однак, номінал облігацій одного класу, як правило, залишається незмінною, тому його впливом на зміну ціни облігації можна знехтувати. Вплив же купонних виплат і терміну погашення на ціну облігації можна в кінцевому рахунку звести до дослідження впливу прибутковості до погашення.
В такому випадку, під волатильністю (мінливістю) ціни облігації розуміється реакція ціни облігації на миттєве, стрибкоподібне зміна її прибутковості до погашення за інших рівних умов.
Реакція ціни облігації на зміну необхідної прибутковості має ряд характерних рис:
1) Залежність між прибутковістю до погашення i і ринковою ціною облігації носить зворотний характер. При цьому, зі зниженням величини i збільшення # 8710; P 0 при одних і тих же зниженнях прибутковості до по гасінню # 8710; i збільшуються.
2) Для одного і того ж терміну погашення облігації, чим вище купонна ставка, тим слабкіше реагує ціна облігації на одні і ті ж зміни прибутковості до погашення. Відповідно, чим нижче купонна ставка, тим сильніше реакція ціни P 0 на одні і ті ж зміни прибутковості до погашення.
3) Якщо купонна ставка відсотка не змінюється, то збільшення терміну погашення облігації викликає більш сильну реакцію ціни P 0 облігації на одні і ті ж зміни її прибутковості до погашення i.
4) Невеликі зміни прибутковості до погашення призводять до однакових змін ціни облігації в обох напрямках. Іншими словами, якщо прибутковість i зростає на незначну величину, то це призводить до такого процентному зменшенню ціни P 0, яке приблизно дорівнюватиме відсоткового підвищення P0 при такому ж незначному зниженні i.
Прогнозування є стрижнем будь-якої торгової системи, в зв'язку з цим грамотно зроблені прогнози Forex можуть зробити вас аспідскі грошовим.
5) Значні зміни прибутковості до погашення i викликають асиметричну реакцію цін облігації: якщо прибутковість до погашення зростає на кілька відсотків (наприклад, 2%), то викликане цим зниження ціни облігації буде в процентному відношенні менше за абсолютною величиною процентного збільшення ціни облігації при зниженні прибутковості до погашення на ті ж 2%.
6) При заданому рівні зміни прибутковості до погашення # 8710; i, чим нижче початкова прибутковість до погашення, тим вище реакція ціни на зміни i.
Підсумовуючи все шість властивостей волатильності ціни облігації, можна помітити, що на неї великий вплив мають п'ять факторів:
а) рівень прибутковості до погашення;
б) розмах змін прибутковості до погашення;
в) спрямування цих змін;
г) величина купонної ставки;
д) термін погашення.
Прийнято вважати, що дюрація характеризує "середній термін погашення" всього потоку грошових виплат, які забезпечуються облігацією. Сам Маколі визначав тривалість як "середній зважений термін по гасіння грошових потоків облігації, де" вагами "служать наведені вартості цих потоків грошей". Іншими словами, якщо відомі тимчасові моменти t 1, t 2, t 3. tn. після яких інвестор отримує купонні виплати З 1. С2, С3. З n і номінал Mn. то дюрація це середньозважена величина цих проміжків часу по частках ціни Pi. яку вносить відповідний грошовий потік (купонна виплата і номінал) в початкову вартість P 0 облігації.
Дюрація будь облігації вираховується за формулою:

Отже, тривалість бескупонних облігацій завжди дорівнює строку погашення цієї облігації n років.
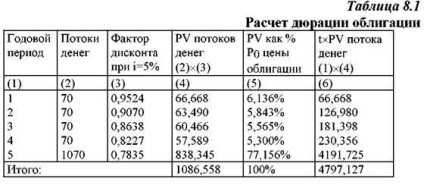
Складніше обчислити дюрації для купонної облігації. Припустимо, що інвестор бажає визначити тривалість купонної облігації номінальною вартістю 1000 рублів, терміном погашення 5 років, з купонним відсотком 7%, що виплачуються щорічно, і прибутковістю до погашення i = 5%. Ціна такої облігації:
Для обчислення D знайдемо фактори дисконту і наведені вартості потоків грошей, які забезпечуються облігацією (в таблиці дані по потокам грошей в рублях):

Властивості дюрації. Дюрація залежить від наступних факторів:
а) прибутковості до погашення;
б) терміну погашення;
в) відсотка купонних виплат. Як правило:
П тривалість D бескупонних (чисто дисконтних) облігацій завжди дорівнює їх терміну погашення;
П D купонних облігацій завжди нижче їх терміну погашення T. При цьому, якщо величина періодичних купонних виплат залишається незмінною, то з підвищенням терміну погашення T = nxt відмінність між тривалістю D і терміном Т зростає.
# 9633; як правило, для одного і того ж терміну погашення D облігації буде тим нижче, чим вище величина купонних виплат (і навпаки). Дана властивість може порушуватися при високих значеннях прибутковості до погашення i і значному терміні погашення;
П якщо величини купонних виплат Ct і прибутковості до погашення i ос таются незмінними, то тривалість D облігації як правило віз розтане зі збільшенням її терміну погашення Т. Позитивна взаємозв'язок між величинами T і D спостерігається для всіх облігацій, крім тих, які мають високі значення i з великим терміном Т.
П П ри незмінних величинах купонних виплат Q і терміну погашення Т,
чим нижче величина прибутковості до погашення i. тим вище значення тривалості D.
Величину [(D) / (1 + i)] прийнято називати модифікованою дюрацією (МД). тоді:
процентна зміна P 0 ≈ МД × (% зміни i) (знак "мінус" свідчить, що зміни величин i і Po відбувається в зворотному напрямку: збільшення i призводить до падіння Po. а зниження i - до зростання Po).
Метод використання модифікованої дюрації МД для оцінки процентного зміни ціни облігацій при коливаннях ринкової процентної ставки (що знайде відображення у змінах прибутковості до погашення) дає більш точні результати в разі його застосування для щодо короткострокових облігацій з високими ставками купонних виплат, ніж для довгострокових облігацій з низькими купонними виплатами.