Родоначальником теорії графів вважається Леонард Ейлер. У 1736 році в одному зі своїх листів він формулює і пропонує рішення задачі про сім Кенігсбергськая мостах, що стала згодом однією з класичних задач теорії графів.
1. У графі, що не має вершин непарних ступенів, існує обхід всіх ребер (причому кожне ребро проходиться в точності один раз) з початком в будь-якій вершині графа.
2. У графі, що має дві і тільки дві вершини з непарними ступенями, існує обхід з початком в одній вершині з непарної ступенем і кінцем в інший.
3. У графі, що має більше двох вершин з непарної ступенем, такого обходу не існує.
Існує ще один вид завдань, пов'язаних з подорожами вздовж графів. Мова йде про завдання, в яких потрібно відшукати шлях, що проходить через всі вершини, причому не більше одного разу через кожну. Цикл, що проходить через кожну вершину один і тільки один раз, носить назву гамільтонової лінії (в честь Вільяма Роуена Гамільтона, знаменитого ірландського математика минулого століття, який першим почав вивчати такі лінії). На жаль, поки що не знайдено спільної критерій, за допомогою якого можна було б вирішити, чи є даний граф Гамільтона, і якщо так, то знайти на ньому все Гамільтона лінії.
Сформульована в середині 19 ст. проблема чотирьох фарб також виглядає як розважальна завдання, проте спроби її рішення призвели до появи деяких досліджень графів, що мають теоретичне і прикладне значення. Проблема чотирьох фарб формулюється так: "Чи можна область будь-якій плоскій карти розфарбувати чотирма кольорами так, щоб будь-які дві сусідні області були розфарбовані в різні кольори?". Гіпотеза про те, що відповідь ствердна, була сформульована в середині 19в. У 1890 році було доведено більш слабке твердження, а саме, що будь-яка плоска карта розфарбовується в п'ять кольорів. Зіставляючи будь-якій плоскій карті двоїстий їй плоский граф, отримують еквівалентну формулювання задачі в термінах графів: Чи правда, що хроматичної число будь-якого плоского графа менше або дорівнює чотирьох? Численні спроби вирішення завдання вплинули на розвиток ряду напрямків теорії графів. У 1976 році анонсовано позитивне рішення задачі з використанням ЕОМ.
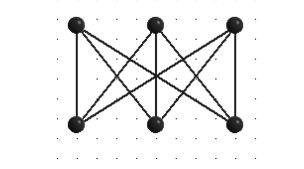
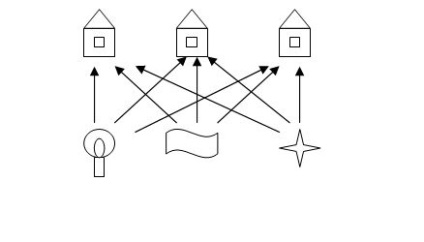
Інша стара топологічна завдання, яке особливо довго не піддавалася вирішенню і розбурхувала розуми любителів головоломок, відома як "задача про електро -, газо - і водопостачання". У 1917 році Генрі Е.Дьюдені дав їй таке формулювання. У кожен з трьох будинків, зображених на малюнку, необхідно провести газ, світло і воду.
Теорія графів. 1
Історія виникнення теорії графів. 1
Правило Ейлера. 1
1. Бєлов Теорія графів, Москва, «Наука», 1968.
3. Кузнецов О.П. Адельсон-Бєльський Г.М. Дискретна математика для інженера. - М. Вища школа. 1988.
6. Оре О. Теорія графів. - М. Наука. 1980.