"Колись мені було запропоновано завдання про острів, розташованому в місті Кенігсберзі і оточеному річкою, через яку перекинуто сім мостів. Питається, чи може хто-небудь безперервно обійти їх, проходячи тільки одного разу через кожен міст. І тут же мені було повідомлено, що ніхто ще до сих пір не міг це зробити, але ніхто і не довів, що це неможливо. Питання це, хоча і банальний, здався мені, проте, гідним уваги тим, що для його вирішення недостатні ні геометрія, ні алгебра, ні комбинаторное мистецтво ... після довгих роздумів я н йшов легке правило, засноване на цілком переконливому доказі, за допомогою якого можна у всіх завданнях такого роду відразу ж визначити, чи може бути здійснений такий обхід через яке завгодно число і як завгодно розташованих мостів або не може. Кенигсбергских ж мости розташовані так, що їх можна уявити на наступному малюнку [рис.1], на якому A позначає острів, а B, CіD - частини континенту, відокремлені один від одного рукавами річки. Сім мостів позначені буквами a, b, c, d, e, f, g " .
З приводу виявленого їм способу вирішувати завдання подібного роду Ейлер писав [см. [5] стор. 102-104]:
"Це рішення за своїм характером, мабуть, має мало відношення до математики, і мені незрозуміло, чому слід швидше від математика очікувати цього рішення, ніж від будь-якої іншої людини, бо це рішення підкріплюється одним тільки міркуванням, і немає необхідності залучати для знаходження цього рішення будь-які закони, властиві математики. Отже, я не знаю, яким чином виходить, що питання, які мають зовсім мало відношення до математики, швидше за дозволяється математиками, ніж іншими ".
Так чи можна обійти Кенигсбергских мости, проходячи тільки один раз через кожен з цих мостів? Щоб знайти відповідь, продовжимо лист Ейлера до Маринони:
0 "Питання полягає в тому, щоб визначити, чи можна обійти всі ці сім мостів, проходячи через кожен тільки один раз, або не можна. Моє правило призводить до наступного вирішення цього питання. Перш за все, потрібно дивитися, скільки є дільниць, розділених водою, - таких, у яких немає іншого переходу з одного на інший, крім як через міст. В даному прикладі таких ділянок чотири - A, B, C, D. Далі потрібно розрізняти, чи є число мостів, що ведуть до цих окремих дільницях, парних або непарних . Так, в нашому випадку до ділянки A ведуть п'ять мостів, а до остальн м - за три мости, т. е. Число мостів, що ведуть до окремих ділянок, непарній, а цього одного вже досить для вирішення задачі. Коли це визначено, застосовуємо наступне правило: якщо б число мостів, що ведуть до кожній окремій ділянці, було парних , то тоді обхід, про який йде мова, був би можливий, і в той же час можна було б почати цей обхід з будь-якої ділянки. Якщо ж з цих чисел два були б непарні, бо тільки одне бути непарною не може, то й тоді міг би відбутися перехід, як це наказано, але тільки початок обходу неодмінно має бути взято від одного з тих двох ділянок, до яких веде непарне число мостів. Якби, нарешті, було більше двох ділянок, до яких веде непарне число мостів, то тоді такий рух взагалі неможливо ... якщо можна було привести тут інші, більш серйозні завдання, цей метод міг би принести ще більшу користь і їм не варто було б нехтувати " .
Математик писав, що перехід можливий, якщо на ділянці розгалуження річки є не більше двох областей, в які веде непарне число мостів. Для того, щоб простіше уявити собі це, будемо прати на малюнку вже пройдені мости. Легко перевірити, що якщо ми почнемо рухатися відповідно до правил Ейлера, перетнемо один міст і зітремо його, то на малюнку буде зображений ділянку, де знову є не більше двох областей, в які веде непарне число мостів, а при наявності областей з непарним числом мостів ми будемо розташовуватися в одній з них. Продовжуючи рухатися так далі, пройдемо через всі мости по одному разу.
Історія з мостами міста Кенігсберга має сучасне продовження. Відкриємо, наприклад, шкільний підручник з математики під редакцією Н.Я. Виленкина для шостого класу. У ньому на сторінці 98 в рубриці розвитку уважності і кмітливості ми знайдемо завдання, що має безпосереднє відношення до тієї, яку колись вирішував Ейлер.
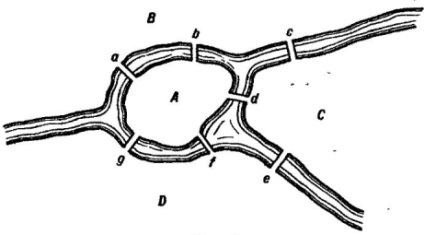
Завдання № 569. На озері знаходиться сім островів, які з'єднані між собою так, як показано на малюнку 1.2. На який острів повинен доставити мандрівників катер, щоб вони могли пройти по кожному мосту і тільки один раз? Чому не можна доставити мандрівників на острів A?
Рішення. Оскільки ця задача подібна завданню про Кенигсбергских мостах, то при її рішенні ми також скористаємося правилом Ейлера. В результаті отримаємо таку відповідь: катер повинен доставити мандрівників на острів E або F. щоб вони змогли пройти по кожному мосту один раз. З того ж правила Ейлера випливає неможливість необхідного обходу, якщо він почнеться з острова A.
На закінчення відзначимо, що задача про Кенигсбергских мостах і подібні до неї завдання разом з сукупністю методів їх дослідження становлять дуже важливий в практичному відношенні розділ математики, званий теорією графів. Перша робота про графах належала Л. Ейлера і з'явилася в 1736 році. Надалі над графами працювали Кеніг (1774-1833), Гамільтон (1805-1865), з сучасних математиків - К. Берж, О. Оре, А. Зиков.