Сьогодні ми поговоримо про таку спочатку уявній тривіальної речі як сортування. Дуже часто можна бачити, що її вчать і викладають, як і тему рекурсії, тобто практично не вчать і не викладають :). А в книгах серій «для чайників» і взагалі в більшості книг цьому питанню не приділяється абсолютно ніякої уваги, тому як там все направлено на швидкий ефект.
Виходить цікава річ, люди можуть збирати складні структури баз даних, використовують багатопоточність і т.п. але сортування, управління чергами, стеками, масивами даних для них є чимось архіскладних. Багато посперечаються зі сказаним, але можу запитати, ви бачили, як використовується сортування, коли програма підвисає? Скажімо, в рамках погано налагоджених розробок нерідко. Всі вже звикли до високорівневих моделей, і в ряді випадків люди використовують заздалегідь підготовлені методи, хоча їх внутрішню структуру представляють насилу. Тим часом принципи сортування потрібно знати, особливо програмістам ІІ.
Взагалі, життя показує цікаві речі. В середині 90-х, коли я виконував замовлення, то зберігав бази даних в текстових файлах (з символьними роздільниками або без оних), а управління цієї структури реалізовувалося за рахунок функцій тієї чи іншої мови. Потім я уважно подивився на HTML, і вирішив, що html-теги вельми зручно використовувати в якості символьних роздільників. І тільки через кілька років з'явився такий стандарт як XML. Тобто, думки зійшлися, і виходить, що я свого часу розробив і використовував технологію майбутнього. Зараз я зберігаю бази даних в підвантажуваних виконуваних Lua-файлах, в яких містяться не тільки самі дані, але і всі методи, які можна до них застосувати, а також взаємопов'язувати структури. Їх наповнення можна змінювати динамічно.
Створити свою власну структуру бази даних і реалізувати систему управління нею взагалі не складно насправді, але користувачі-програмісти звикли витрачати багато часу на вивчення і використання вже готових технологій.
Поговоримо про сортування. Розроблено багато алгоритмічних моделей, тобто, тема досить добре вивчена, але варто відзначити той момент, що потрібно знати базові принципи, а в кожному окремому випадку тієї ж сортуванням можна управляти.
Перед тим як вирішувати питання сортування необхідно знати обсяг даних, які необхідно обробляти. Є методи, які найбільш ефективні при малій кількості елементів, але вони стають досить громіздкими при великому. Також є і спеціальні методи, один з яких ми розглянемо в кінці матеріалу.
Простий метод - бульбашкова сортування
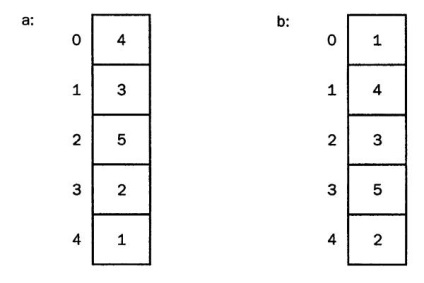
Бульбашкова сортування. a - початковий масив; b - четвертий елемент «спливає» на поверхню.
Назва цього методу описову, тобто мається на увазі що спливає на поверхню води пухирець повітря. В принципі, це гарне і зрозуміле порівняння.
Уявіть собі цілочисельний масив, що складається, наприклад, з п'яти елементів. Вам потрібно розставити їх в порядку зростання значень чисел, тобто, data [0] буде містити мінімальну кількість, а data [4] максимальне з наявних. Що відбувається в рамках цього алгоритму. Спочатку, верхній елемент data [4] порівнюється з попереднім data [3], і якщо його значення менше, елементи міняються місцями. І так далі, поки мінімальний елемент не спливе як бульбашка повітря. Фактично, все сказане буде простіше описати кодом:
if (array [i-1]> array [j]) swap (array, i-1, j);
size - ця величина масиву, але в рамках циклу ми беремо значення size-1 оскільки максимальний елемент автоматично займає свою позицію. Внутрішній цикл for проходить в зворотному по відношенню до зовнішнього напрямку, хоча можна робити і в прямому.
Метод бульбашкового сортування має один недолік - велика кількість дій, тобто, він ресурсномісткий. При цьому, проаналізувавши ви можете сказати, в чому полягає основна проблема - переміщення елементів всього на одну позицію.
Простий метод - вибіркова сортування
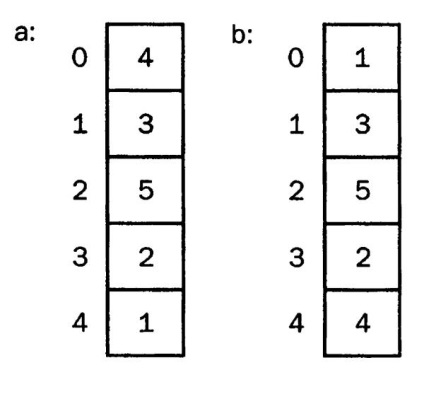
Вибіркова сортування. Тут показано як останній елемент масиву міняється місцями з першим.
А чи можна зробити так, щоб елемент порівнювався з усіма наявними, і при задоволенні умов ставав на позицію data [0], здійснюючи тільки єдиний обмін? Так, саме так працює вибіркова сортування. Вона є вдосконаленим варіантом бульбашкового. Тобто, спочатку з усього масиву відшукується мінімальне значення, визначається його індекс. Після цього міняються місцями data [0] і data [індекс мінімального значення]. Потім береться наступний подмассів, в якому вже не враховується data [0], і ми заповнюємо мінімальним значенням data [1] і так далі.
У коді це писати трохи об'ємно (за що часто лають журналістів ІТ-ЗМІ :)), тому скажемо, що нам знадобиться один внутрішній цикл, в якому ми знаходимо значення індексу елемента, що містить мінімальну кількість, а після робимо перестановку. Потім виробляємо такий же пошук в підмасиві і так далі, що робиться в зовнішньому циклі. При цьому, код оптимізується обмеженням того, що перестановка проводиться в разі, якщо переставляється елемент не містить мінімальне значення, тобто if (min_index! = I).
Складний метод - швидке сортування
Швидке сортування є одним з найбільш ефективних методів, а по суті це дві взаємопов'язаних сортування. Суть методу полягає в тому, що з масиву вибирається який-небудь елемент, який буде виступати в якості розділяє значення. Розділяє (!) - це означає, що воно буде розділяти. А що саме? Насправді, мається на увазі двостороннє рух від початку масиву і його кінця, по термінології простіше застосовувати назви Head (голова) та Tail (хвіст). Тобто, якщо ми говоримо про розстановку чисел по зростанню, алгоритм сортування в Head буде порівнювати числа на умова> розділяє значення (якщо «так», то це велике значення змінюється з розділяє), а алгоритм сортування в Tail буде порівнювати числа на умова <разделяющего значения (если «да», то это большое значение меняется с разделяющим). В момент когда Head и Tail сходится на одном элементе (место пересечения указателей), мы можем сказать, что все что справа (или ниже) меньше разделяющего значения, а все, что слева(сверху) — больше.
Потім ці дві частини упорядковано відповідно до окремо таким же чином (функція сортування рекурсивно викликає саму себе).
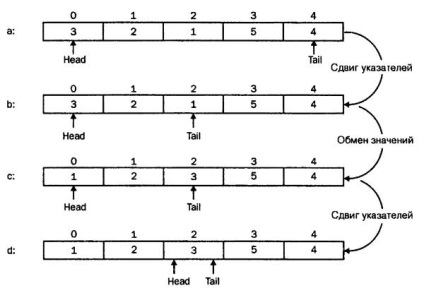
Швидке сортування. Як розділяє значення вибрано 3 (крайнє ліве значення). Tail, дійшовши до одиниці (b) стикається з умовою «поточне значення <разделяющего», Происходит обмен. Потом идет проверка со стороны Head, так как ситуация изменилась, указатели пересекаются на элементе массива a[2]. Следующим этапом будет идентичная обработка правой и левой частей.
Швидкий алгоритм часто супроводжують фразою: «розділяй і володарюй». Це так, але дуже багато залежить від вибору розділяє елемента / значення. Наприклад, масив містить -3,5,0,7,2. Спробуйте самі вибрати значення, яке забезпечить максимально швидку сортування (найбільш зручним варіантом при першому циклі сортування виявиться 0 або 2) і найбільш повільну (коли для першого циклу сортування ви оберете в якості розділяє максимальне або мінімальне значення, тобто -3 або 7 ). Найбільш вигідною ситуацією також буде, коли масив ділиться на дві рівні частини.
Також уважно придивившись, ви виявите, що в ряді випадків швидке сортування не вигравали в порівнянні простими методами, про які ми написали. А найбільший мінус буде в разі, коли ми застосуємо швидку сортування до вже відсортовані масиву.
Взагалі, методів швидкого сортування існує кілька, їх основна відмінність полягає в алгоритмі вибору розділяє значення (процедурі розбиття), оптимізації рекурсії.
У швидкого сортування є і ще один веселий мінус - входження в нескінченність. Тобто, масив 3,2,3 призведе до критичної ситуації, тому як потрібна процедура обробки повторюваних значень, чого в стандартних алгоритмах не передбачено.
Складний метод - поліпшена швидке сортування
Покращена швидке сортування більш точно підходить до вибору значення поділу. Потрібно визначитися з медіаною масиву, тобто серединним значенням в загальному спектрі. Її визначення досить затратно, але чим більша кількість значень потрібно обробляти, тим краще виходить баланс витрачених ресурсів.
Для визначення медіани зазвичай знаходиться середнє значення між двома крайніми і серединним елементами. Для вирішення ситуації з повторюваними значеннями передбачена спеціальна процедура, яка використовує конструкції if (...<=… или …>= ...) або ж просто обігрується ситуація в разі виникнення рівності.
Складний метод - сортування злиттям
Сортування злиттям має на увазі функцію сортування з розбивкою масиву навпіл - на два подмассіва, після функція сортування викликає себе рекурсивно для кожної з половин, після чого об'єднує сортовані подмассіви в один масив. Вся робота по сортуванню проводиться в міру розмотування стека викликів. Для функціонування алгоритму потрібен додатковий тимчасовий масив того ж розміру, що й вихідний, який після копіюється в основний.
Сортування злиттям краще поліпшеною швидкого сортування в силу простоти (не потрібно ніяких поділяють елементів і схрещування покажчиків), а також в ній не виникає проблеми найгіршого випадку, який може з'явитися при швидкій сортування.
Складний метод - «дискретна сортування»
На моїй пам'яті я її зустрічав тільки кілька разів. Втім, він одного разу мені знадобився, тому я такий розробив і сам. По суті даний алгоритм працює як ... АЦП і кілька інших відомих алгоритмів. Тобто, спочатку в масиві шукається максимальне і мінімальне значення. Потім обчислюється середнє з них, тобто, діапазон значень / 2. Після цього всі елементи проходять порівняння з цим значенням, і ті, що менше, заносяться в ліву частину, ті, що більше - в праву. Створюється тимчасовий масив таких же розмірів, що і вихідний, в якому елементи, що містяться зліва отримують індекси, починаючи з нуля, а ті які зліва - з [загальна кількість ел-тів - поточний індекс для правої частини].
Потім (для кожної з половин ми вже знаємо їх середні значення 1/4 діапазону і 3/4 діапазону значень, а також кількість елементів у кожній з половин), ми також проводимо порівняння із середніми значеннями половин, і так далі, поки не доходимо до одного елемента. Після цього йде збірка з відповідною розстановкою індексів. «Дискретна сортування» як і сортування злиттям вимагає наявності додаткового масиву, тобто, так би мовити, виконується не "за місцем».
Не сказати, що алгоритм дискретної сортування трудомісткий у виконанні, хоча є і складні варіанти виконання. Він надійний, але досить ресурсоемок. Добре застосуємо для випадків неоднорідних масивів, в яких присутні «порожнечі», тобто, наприклад, діапазон значень від 0 до 100, а основна маса значень елементів зосереджена в інтервалі 80-90. А взагалі, основна принада дискретної сортування і її методів проявляється у випадках, коли потрібно округляти значення, відстежувати певні ділянки динамічно поповнюються масивів і так далі.
Як бачите, особливо складного в рамках сортування Нічого придумано не було. Потрібно тільки уважно придивитися. Самі алгоритми досить добре полегшуються в умовах, коли ви добре розбираєтеся у внутрішній структурі завдання. Наприклад, якщо в загальному випадку той чи інший алгоритм описується як ресурсномісткий і розташовує до помилок, то в приватному він може бути найбільш ефективним при правильній розстановці обмежень.
В наступній частині матеріалу ми поговоримо про стек і рекурсії, оптимізації рекурсії.