У формулі (6) векторна норма означає відстань вершини до центру ваги комплексу. а сама формула (6) визначає середнє відстань вершин комплексу до його цента тяжкості.
У формулі (7) є середнє значення функції () в вершинах комплексу. а сама формула (7) визначає середнє відхилення значень функції () в вершинах комплексу від цього середнього значення.
Метод комплексів ілюструє рис. 3, на якому показаний фрагмент ліній рівня функції Гіммельблау. На малюнку вихідний комплекс має вершини. [1, 4]. Після відображення з розтягуванням вершини цього комплексу, в якій функція має максимальне значення, отримуємо комплекс з вершинами. [1, 4]. Після відображення з розтягуванням вершини комплексу. в якій функція має максимальне значення, отримуємо комплекс з вершинами. [1, 4].
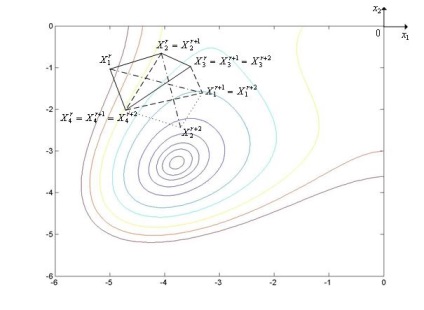
Мал. 3. Траєкторія пошуку мінімуму функції Гіммельблау методом комплексів.
Відомо безліч модифікацій розглянутого методу комплексів, спрямованих, зокрема, на подолання «уплощения» комплексу в процесі пошуку. З цією метою через фіксовану кількість ітерацій знаходяться максимальна і мінімальна діагоналі комплексу і, якщо їх відношення перевищує ліміт, то за розглянутою схемою проводиться побудова нового комплексу.
8.3 Метод повторюваного випадкового пошуку
Розглядається наступна багатовимірна задача локальної безумовної оптимізації: знайти мінімум критерію оптимальності (), визначеного в вимірному евклідовому просторі,
У методі повторюваного випадкового пошуку (трьох-кроковий метод) використовується итерационная схема (див. Рис. 1)