
Прямокутна ізометрична проекція деталі «Втулка», виконана на основі її ортогональних проекцій
Ізометрична проекція - це різновид аксонометрической проекції. при якій в відображенні тривимірного об'єкту на площину коефіцієнт спотворення (відношення довжини спроектованого на площину відрізка, паралельного координатної осі. до дійсної довжині відрізка) по всіх трьох осях один і той же. Слово «ізометрична» в назві проекції прийшло з грецької мови і означає «рівний розмір», відображаючи той факт, що в цій проекції масштаби по всіх осях рівні. В інших видах проекцій це не так.
Ізометрична проекція використовується в машинобудівному кресленні і САПР для побудови наочного зображення деталі на кресленні. а також в комп'ютерних іграх для тривимірних об'єктів і панорам.
Необхідно відзначити, що паралельні проекції. різновидом яких є аксонометричні і, в тому числі, ізометричні проекції, діляться також на ортогональні (перпендикулярні), з направленням проекції перпендикулярним до площини проекції, і косокутні. з кутом між напрямком і площиною, відмінним від прямого. За радянськими стандартами (див. Нижче) аксонометричні проекції можуть бути і ортогональними, і косокутність [1]. В результаті, за західними стандартами ізометрична проекція визначається вужче і, крім рівності масштабів по осях, включає умову рівності 120 ° кутів між проекціями будь-якої пари осей. Щоб уникнути плутанини далі, якщо не вказано інше, під ізометричної проекцією буде матися на увазі тільки прямокутна ізометрична проекція.
Прямокутна (ортогональна) ізометрична проекція
У прямокутної ізометричної проекції аксонометричні осі утворюють між собою кути в 120 °, вісь Z 'спрямована вертикально. Коефіцієнти спотворення (k x. K y. K z, k_, k_>) мають числове значення 2 3 ≈ 0. 82 >> \ approx 0,82>. Як правило, для спрощення побудов изометрическую проекцію виконують без спотворень по осях, тобто коефіцієнт спотворення приймають рівним 1, в цьому випадку отримують збільшення лінійних розмірів в 1 0. 82 ≈ 1. 22> \ approx 1,22> рази.
Косокутна фронтальна ізометрична проекція
Вісь Z 'спрямована вертикально, кут між віссю X' і Z 'дорівнює 90 °, вісь Y' з кутом нахилу 135 ° (допускається 120 ° і 150 °) від осі Z '.
Фронтальна ізометрична проекція виконується по осях X ', Y' і Z 'без спотворення.
Криві, паралельні фронтальній площині, проектуються без спотворень.
Косокутна горизонтальна ізометрична проекція
Вісь Z 'спрямована вертикально, між віссю Z' і віссю Y 'кут нахилу дорівнює 120 ° (допускається 135 ° і 150 °), при цьому зберігається кут між осями X' і Y 'рівним 90 °.
Горизонтальну ізометричну проекцію виконують без спотворення по осях X ', Y' і Z '.
Криві, паралельні горизонтальній площині [2] проектуються без спотворень.
Варто відзначити, що, оскільки ортогональний тригранників неможливо повернути так, щоб два його ребра були б видно взаємно-перпендикулярними, і третє ребро при цьому не проектувалася б в точку, все проекції, в яких видно всі три осі, але кут на кресленні між до -н двома - прямий (тут це друга і третя з наведених), строго кажучи, показують «те, чого не буває».
На щастя, очей людини досить успішно коригує такі похибки при зображенні реальних об'єктів, і тому вони допустимі заради простоти побудови креслення.
Ізометричний вид об'єкта можна отримати, вибравши напрямок огляду таким чином, щоб кути між проекцією осей x. y. і z були однакові і рівні 120 °. Наприклад, якщо взяти куб, це можна виконати направивши погляд на одну з граней куба, після чого повернув куб на ± 45 ° навколо вертикальної осі і на ± arcsin (tan 30 °) ≈ 35,264 ° навколо горизонтальної осі. Зверніть увагу: на ілюстрації ізометричної проекції куба контур проекції утворює правильний шестикутник - все ребра однакової довжини і всі грані дорівнює площі.
Інший шлях візуалізації ізометричної проекції полягає в розгляді виду кубічної кімнати з верхнього кута з напрямком погляду в протилежний нижній кут. Ось x тут спрямована діагонально вниз і вправо, вісь y - діагонально вниз і вліво, вісь z - прямо вгору. Глибина також відбивається висотою картинки. Лінії, намальовані вздовж осей, мають кут 120 ° між собою.
Є 8 різних варіантів отримання ізометричної проекції в залежності від того, в який октант дивиться спостерігач. Ізометричне перетворення точки a x. y. z> в тривимірному просторі в точку b x. y> на площині при погляді в перший октант може бути математично описано за допомогою матриць повороту наступним чином. Спочатку, як пояснено в розділі Візуалізація. виконується поворот навколо горизонтальної осі (тут x) на α = arcsin (tan 30 °) ≈ 35,264 ° і навколо вертикальної осі (тут y) на β = 45 °:
Інші сім можливих видів виходять поворотом до протистояли сторонам і / або інверсією напрямку погляду. [3]
Обмеження аксонометрической проекції
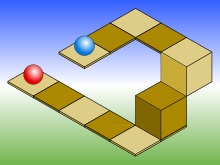
Ізометричний малюнок з блакитною кулею на два рівні вище червоного
Як і в інших видах паралельних проекцій. об'єкти в аксонометрической проекції не виглядають більше або менше при наближенні або видаленні від спостерігача. Це корисно в архітектурних кресленнях і зручно в спрайт-орієнтованих комп'ютерних іграх. але, на відміну від перспективної (центральної) проекції. призводить до відчуття викривлення, оскільки людське око або фотографія працюють інакше.
Це також легко призводить до ситуацій, коли глибину і висоту неможливо оцінити, як показано на ілюстрації справа. У цьому ізометричному малюнку блакитну кулю на два рівні вище червоного, але це не можна побачити, якщо дивитися тільки на ліву половину картинки. Якщо виступ, на якому знаходиться блакитна куля, розширити на один квадрат, то він виявиться точно поруч з квадратом, на якому знаходиться червоний куля, створюючи оптичну ілюзію. ніби обидві кулі на одному рівні.
Додаткова проблема, специфічна для ізометричної проекції - складність визначення, яка сторона об'єкта спостерігається. При відсутності тіней і для об'єктів, які щодо перпендикулярні і відповідні, складно визначити, яка сторона є верхній, нижній або бічний. Це відбувається через приблизно рівних за розміром і площі проекцій такого об'єкта.
Більшість сучасних комп'ютерних ігор уникають цього за рахунок відмови від аксонометрической проекції на користь перспективного тривимірного рендеринга. Однак експлуатація проекційних ілюзій популярна в оптичному мистецтві - такому, як роботи із серії «неможливою архітектури» Ешера. Водоспад (1961) - хороший приклад, в якому будова в основному ізометричне, в той час як бляклий фон використовує перспективну проекцію. Інша перевага полягає в тому, що в кресленні навіть новачки легко можуть будувати кути в 60 ° за допомогою тільки циркуля і лінійки.
Ізометрична проекція в комп'ютерних іграх і піксельної графіку

Малюнок телевізора в майже-ізометричної піксельної графіку. У пиксельного візерунка видно пропорцію 2: 1
В області комп'ютерних ігор і піксельної графіки аксонометрична проекція була вельми популярна в силу легкості, з якою двомірні спрайт і плиткове графіка могли бути використані для подання тривимірної ігрового середовища - оскільки під час переміщення по ігровому полю об'єкти не міняють розмір, комп'ютера не потрібно масштабувати спрайт або виконувати обчислення, необхідні для моделювання візуальної перспективи. Це дозволяло старим 8-бітовим і 16-бітовим ігровим системам (і, пізніше, портативним ігровим системам) легко відображати великі тривимірні простору. І хоча плутанина з глибиною (см. Вище) іноді могла бути проблемою, хороший дизайн гри здатний її пом'якшити. З приходом більш потужних графічних систем аксонометрична проекція стала втрачати свої позиції.
Проекція в комп'ютерних іграх зазвичай дещо відрізняється від «істинної» ізометричної в силу обмежень растрової графіки - лінії по осях x і y не мали б акуратного пиксельного візерунка, якби малювалися під кутом в 30 ° до горизонталі. Хоча сучасні комп'ютери можуть усувати цю проблему за допомогою згладжування. раніше комп'ютерна графіка не підтримувала достатню колірну палітру або не мала достатню потужність процесорів для його виконання. Замість цього використовувалася пропорція пиксельного візерунка 2: 1 для малювання осьових ліній x і y. в результаті чого ці осі розташовувалися під кутом arctg 0,5 ≈ 26,565 ° до горизонталі. (Ігрові системи з неквадратних пікселями могли, однак, приводити до інших кутках, включаючи повністю ізометричні [4]). Оскільки тут з трьох кутів між осями (116,565 °, 116,565 °, 126,87 °) рівні тільки два, такий вид проекції більш точно характеризується як варіація діметріческой проекції. Однак більшість представників спільнот комп'ютерних ігор і растрової графіки продовжує називати цю проекцію «ізометричної перспективою». Також, часто використовуються терміни «вид 3/4 (англ.)» І «2.5D».
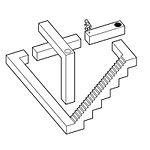
Кадр з гри «echochrome»
Цікавий приклад використання особливостей ізометричної проекції спостерігається в грі echochrome (яп. 無限 回廊 муген кайро:). Слоган гри - «В цьому світі то, що ти бачиш, стає реальністю». Сенс гри полягає в тому, що ілюзія, що виникає при погляді на изометрически побудований тривимірний рівень з певної точки, перестає бути ілюзією. Наприклад, якщо подивитися на рівень таким чином, щоб майданчики, що знаходяться на різній висоті, виглядали так, ніби вони знаходяться на одній і тій же висоті (см. Зображення з синім і червоним кулями з попереднього розділу), грою вони будуть розцінюватися як знаходяться на одній висоті, і людина (гравець) зможе запросто «переступити» з одного майданчика на інший. Потім, якщо повернути карту рівня і подивитися на конструкцію так, щоб було чітко видно різницю в висоті, можна зрозуміти, що насправді людина «переступив» на іншу висоту, користуючись тим, що ізометрична ілюзія на якийсь момент стала реальністю. На наведеному в якості ілюстрації кадрі з гри становище майданчика, що знаходиться вгорі сходів, можна уявити двояко: в одному випадку вона знаходиться на одній висоті з майданчиком, на якій знаходиться гравець (можна переступити), а в іншому випадку - під нею (можна зістрибнути через чорне отвір). Обидва випадки будуть одночасно бути правдою. Очевидно, цей ефект досягається відсутністю перспективи в ізометрії.
Історія изометрических комп'ютерних ігор

Q * bert (1982), одна з перших ігор з ізометричної графікою
Першими іграми, що використовують изометрическую проекцію, були аркадні ігри початку 1980-х: так, Q * bert [11] і Zaxxon (англ.) [12] випущені в 1982 році. Q * bert показує статичну піраміду, намальовану в ізометричної перспективі, по якій повинен стрибати керований гравцем персонаж. Zaxxon пропонує прокручуваний ізометричні рівні, над якими літає керований гравцем літачок. Рік по тому, в 1983 році. була випущена аркадна гра Congo Bongo (англ.) [13]. працювала на тих же ігрових автоматах, що і Zaxxon. У цій грі персонаж переміщається по великим изометрическим рівням, що включає тривимірні підйоми і спуски. Те ж саме пропонується і в аркадной грі Marble Madness (1984).
- Богданов В. Н. Малежик І. Ф. Верхола А. П. та ін. Довідник з креслення. - М. Машинобудування, 1989. - С. 864. - ISBN 5-217-00403-7.
- Фролов С. А. Нарисна геометрія. - 2-е вид. перераб. і доп. - М. Машинобудування, 1983. - С. 240.