
Навігаційна прокладка при наявності дрейфу.
Додамо, що шлях судна при наявності дрейфу - шляховий кут при дрейфі, позначається Пуа. Це як раз шлях, який «показали» наші обсервованние точки. Тобто при веденні навігаційної прокладки, коли ми з'єднували їх лінією, ми визначали Пуа: Пуа = 212 °. ГКК = 225 °. Нагадую, раніше ми домовилися для наочності та простоти розрахунків у веденні навігаційної прокладки, що поправка компаса дорівнює нулю, компасний курс дорівнює істинному курсу: ГКК = ІК. Тут «працює» співвідношення: Пуа = ГКК + α, звідки випливає, що α = Пуа - ГКК = 212 ° - 225 ° = - 13 ° (тобто нас зносить вліво, або ми маємо справу з дрейфом правого галс). Якщо величина α виходить позитивної, нас зносить вправо, або має місце дрейф лівого галс. Запам'ятайте ці речі! Їх потрібно чітко знати кожному яхтсмену!
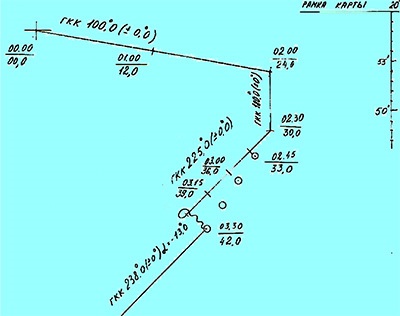
Нам потрібен шлях 225 °. (Пуа = 225 °).
Пуа = α + ГКК. новий ГКК буде:
ГКК = Пуа - α = 225 ° - (-13 °) = 225 ° + 13 ° = 238 °.
Таким чином, нам потрібно лягти на новий курс 238 °. А яхта при цьому буде рухатися по лінії шляху 225 °. Продемонструємо наочно, як оформляється на карті навігаційна прокладка.Обратіте увагу, що тут ми стерли час і відлік лага на момент 03.30 зі старого місця і перенесли на нове, біля обсервованной точки. Це тому, що ми прийняли обсервацію до обліку. До речі, з'явилася і хвиляста лінія, невязка, перекреслює попередній курс.
Ми бачимо також, що шлях судна прокладений так само, як попередній (під тим же кутом). А значення курсу над ним змінилося на тільки що розраховане. І в написи з'явилося значення а = - 13 °. Це говорить про те, що тепер ми маємо справу з колійним кутом при дії дрейфу і даний дрейф ми враховуємо. Для контролю правильності ведення навігаційної прокладки в яхтинг існує правило: сума значень курсу і кута дрейфу повинна скласти значення напряму прокладеній на карті лінії шляху. Це, до речі, відноситься і до випадків, коли діє протягом само по собі і спільно з дрейфом, і коли компас має поправку. Простими словами: складаємо всі цифри, що є (в тому числі і в дужках) на лінії шляху, зі своїми знаками і отримуємо значення кута лінії шляху. Інакше, для контролю навігаційної прокладки на карті, знімаємо з допомогою паралельної лінійки і транспортира напрямок колійного кута з карти. Складаємо все цифри в написи над дорожнім кутом. Обидві величини повинні бути рівні. Інакше в ваші дії вкралася помилка, з якою необхідно негайно розібратися.
Тепер ми будемо вести навігаційну прокладку вже на дорожньому вугіллі Пуа. Так як лаг дрейф враховує, ми просто будемо відкладати РОЛ, відповідні за потрібне нам моментам часу на лінії цього колійного кута. Нічого складного.
А що нам робити при веденні навігаційної прокладки, якщо знову змінювати курс потрібно? Здавалося б, чого простіше? Взяв наведені тут формули, використовуючи відому α = - 13 °, та й розрахував новий курс по необхідному новому подорожнього кутку (Пуа). Але ж ні. У яхтинг не так-то все просто. Справа в тому, що вітрової дрейф виникає, ясна річ, від вітру, що дме в яхту (правда, цікаве висновок?). І сила дії вітру залежить від площі парусності судна (навіть якщо літак не має вітрил, площа його корпусу, надбудов, конструкцій, нестрого кажучи, становить площа парусності). І ще вона залежить від кута, під яким вітер дме щодо діаметральної площині (ДП) самого судна.
З усього сказаного випливає, що в навігаційній прокладці на кожному новому курсі потрібно заново визначати величину зносу від дрейфу. Ось так то! Хіба що, якщо зміни курсу не дуже значні (на практиці в межах 30 ° без перетину лінії вітру), тоді можна для початку використовувати вже певну і обчислену величину α. Але проконтролювати свої розрахунки і місце все-таки потрібно (як завжди в яхтинг!).
 Навігаційна прокладка при наявності течії.
Навігаційна прокладка при наявності течії.

Тепер поговоримо про навігаційної прокладки при перебігу. Це вже складніше буде. Як ми вже говорили, сигналом про те, що на нас діє протягом, є різниця між РОЛ і пройденим по обсервації відстанню за одні й ті ж проміжки часу. Намалюємо, як це буде виглядати на карті.
Зрозуміло, що якби протягом не діяло, обсервованние точки збігалися б з счислімим. Але воно діє. І вектор його дії прямо кидається в очі на нашому малюнку. Швидкість позначимо для цього вектора Vт, курс - Кт. Самі вектора течії показані у вигляді стрілок.
Тепер при веденні навігаційної прокладки побудуємо подібний векторний трикутник для проміжку часу в одну годину, просто для наочності, тому що на ньому вектор швидкості яхти, вектор течії і їх сумарний вектор - вектор шляху під впливом течії, будуть представлені в зручному вигляді в масштабі своїх одиниць виміру. Строго кажучи, те, що ми тут назвали вектором швидкості судна, насправді є вектором передбачуваного шляху човни за приладами, тобто, без урахування течії, як би на спокійній воді. Відзначимо, що швидкість течії вимірюється у вузлах, а його напрямок - в градусах по круговому рахунку.
При визначенні в навігаційної прокладки на карті напрямку течії і роботі з ним, слід знати непорушне правило: протягом «випливає з компаса». Точно так же, як ми визначали напрямки з центру картушки (свого місця) на предмети, будемо відкладати і напрямку течії. Припустимо, напрямок 120 °. Так і відкладемо, від нас через точку на картушке з відміткою 120 °. (Графічно - прокладемо за допомогою лінійки і транспортира кут 120 ° там, де нам потрібно).
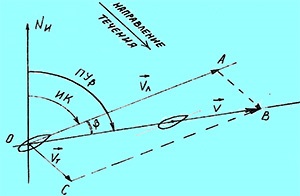
При наявності течії яхта, разом з масами води, зноситься у напрямку течії ОС зі швидкістю V т. Вектор Vт. Фактично ж судно переміщається по лінії ОВ і вектор швидкості такого переміщення є ні чим іншим, як сумою векторів швидкості і течії. Вектор V. Це вектор істинної швидкості яхти.
При цьому слід звернути увагу, що сам кут курсу (тобто положення діаметральноїплощині судна щодо істинного меридіана) залишається колишнім, а напрямок його істинного руху не збігається з площиною ДП. Яхта рухається як би «боком». Лінія, ОВ, по якій рухається судно, називається лінією шляху судна на протязі при веденні навігаційної прокладки.
Кут між лінією шляху і напрямком на істинний меридіан називається колійним кутом і позначається ПУβ.
Кут між істинним курсом судна і колійним кутом називається кутом зносу течією (або кутом знесення від перебігу). Позначається він - β.
Якщо яхту зносить вправо від курсу (течія в цьому випадку направлено в лівий борт) кут зносу вважається позитивним і йому приписується при розрахунках в навігаційної прокладки знак «+». Якщо ж, навпаки, протягом направлено в правий борт, а яхту зносить вліво, той кут зносу - негативний і його враховують зі знаком «-».
Між усіма цими кутами існують співвідношення, суть яких зрозуміла з рисунка.
ПУβ = ІК + (± (β)
ІК = ПУβ - (± (β)
β = ПУβ - ІК.
При веденні навігаційної прокладки на карту наносять лінію фактичного переміщення судна, тобто відкладають ПУβ. З точки початку числення тонкою лінією прокладають лінію ІК, яка використовується в розрахунках. Саме на лінії ІК відкладаються відстані, пройдені яхтою по лагу! Для того, щоб отримати численне точку. з точки на лінії ІК, отриманої при відкладанні пройденого по лагу відстані, що відноситься до відповідного моменту часу, у напрямку течії проводять до перетину з лінією ПУβ пряму. Точка перетину цієї прямої і лінії ПУβ і є наша счислімим точка.
Пряма задача навігаційної прокладки при перебігу.
Але це ми трохи забігли вперед. Адже нам, для проведення вищеописаних маніпуляцій навігаційної прокладки, потрібно спочатку побудувати сам шляховий кут - ПУβ. При цьому нам відомі швидкість і курс судна, а також швидкість і напрямок течії. Таке завдання по навігації в яхтинг носить назву пряме завдання. (Пряма задача навігаційної прокладки - знаходження лінії шляху, істинної швидкості судна і кута зносу при відомих курсах і швидкості судна, і напрямку і швидкості течії). Для вирішення будують навігаційний трикутник. Він такий же, як на попередньому малюнку, тільки оформляється відповідним чином. Демонструємо.
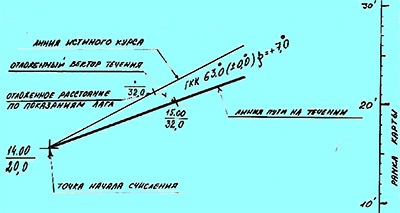
1). З точки початку навігаційної прокладки на карті проводимо тонкою лінією істинний курс судна. Відзначаємо момент часу і відповідний йому відлік лага.
2). Після проходження певного проміжку часу (в нашому прикладі це 1 година), помічаємо відлік лага і знаходимо пройдене за цей час по лагу відстань. Відкладаємо отримане значення на лінії ІК.
3). З отриманої щойно на ІК точки прокладаємо лінію по відомому нам напрямку течії.
4). На відкладеної лінії течії з точки, відповідної пройденого по лагу відстані (яка у нас знаходиться на лінії ІК) відкладаємо вимірником відому нам швидкість течії.
5). З точки початку навігаційної прокладки через отриману в п.4 точку проводимо пряму лінію (товщі лінії ІК). Це і буде лінія шляху на численні.
У нашому прикладі навігаційної прокладки ми використовували проміжок часу в 1 годину (моменти 14.00 і 15.00). Таким чином, ми просто з кінця вектора швидкості судна відклали вектор течії і отримали сумарний вектор знесення. На практиці ж в яхтинг такі побудови буває потрібно зробити за коротший період. Сам принцип дій при цьому залишається тим самим, але ми відкладаємо вже не відстань, пройдену судном за годину, а відстань, пройдену саме за потрібний нам проміжок часу. Природно, з отриманої точки ми також не будемо відкладати вектор течії, як такої, а то відстань яке воно «проходить» за цей проміжок часу.
Зворотній завдання навігаційної прокладки при перебігу.
А звідки, взагалі беруться значення напрямку і швидкості течії? Так з карти і беруться, а також з навігаційних посібників. Але течія - штука примхлива і непостійна. Нерідко наведена інформація про нього виявляється, як мінімум, неточною. Тому при навігаційної прокладки в яхтинг його елементи найчастіше доводиться уточнювати, а то і визначати з самого початку самим, якщо є можливість точно визначати місцеположення свого судна. Про це трохи пізніше, коли будемо розглядати сумарну дію дрейфу і течії. А поки поговоримо про зворотній задачі навігаційної прокладки при перебігу. Вона полягає в тому, що нам вже відомий кут шляху яхти. швидкість судна по лагу і елементи самого перебігу (його курс і швидкість). А знайти потрібно значення курсу, істинної швидкості судна і кута зносу β.
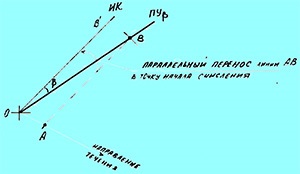
2) З цієї ж точки відкладаємо напрямок течії.
3) За його напрямку відкладаємо величину швидкості течії (якщо будуємо трикутник для проміжку часу в 1 годину). Якщо у нас інший проміжок часу, то відкладаємо величину відстані, яке як би «пройшло» протягом за даний проміжок. Отримуємо точку А.
4) З отриманої точки (кінця вектора течії) розчином циркуля, що дорівнює відстані, пройденого судном за наш проміжок часу, відкладаємо на прокладеній лінії шляху судна на протязі точку. Отримуємо точку В.
5). Напрямок АВ паралельної лінійкою переносимо в точку початку ведення навігаційної прокладки. Отримуємо пряму ОВ, яка і буде лінією істинного курсу нашої судна. Завдання вирішена. Кут зносу - кут між ПУβ і ІК.
Прийшов, нарешті, час поговорити про спільне обліку дрейфу і течії в навігаційної прокладки. На практиці в яхтинг найчастіше яхтсменам доводиться стикатися саме з такою ситуацією. Ці побудови будуть ще трішки складніше. Однак, лякатися не варто. Але про це в наступній статті.