літі матрицю на скалярну величину. Хоча поділ матриці на іншу матрицю не визначене строго, матрицю завжди можна розділити на скалярну величину. Такий поділ полягає в розподілі кожного елемента матриці на дане число.
Матриці - це векторні математичні об'єкти, що містять 2 або більше скалярних елемента. Матриці використовуються для знаходження багатьох невідомих в системах скалярних рівнянь, і для операцій з великими масивами чисел. Як і зі скалярними величинами (наприклад, числами 1, 2, 3, 4), з векторами можна робити математичні обчислення, такі як додавання, віднімання і множення. Однак матриці можна безпосередньо розділити одну на іншу. Для поділу матриць необхідно провести дію, що складається з двох етапів. Спочатку визначається матриця, зворотна делителю (знаменника). Потім на цю матрицю множиться та, яку ділять, або матриця-чисельник. Такий метод дозволяє отримати шуканий результат, не проводячи розподіл безпосередньо. У цій статті розповідається, як ділити матриці.
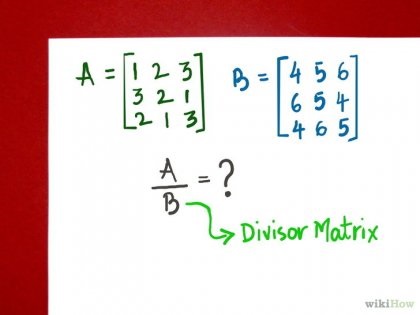
Визначте матрицю, зворотну матриці-знаменника. Методи знаходження зворотних матриць та інших дій з матрицями можна знайти в підручниках і довідниках з математики. Обчисліть детермінант матриці-знаменника. Процедура знаходження детермінанта матриці описана в математичних підручниках. Мета цього кроку полягає в тому, щоб визначити, відмінний чи детермінант матриці від нуля. Якщо детермінант матриці-подільника дорівнює нулю, це означає, що дана матриця необоротна, тобто для неї не існує оберненої матриці. У цьому випадку припиніть подальші дії. Якщо матриця, зворотна матриці-делителю не існує, далі можна не продовжувати. Така ситуація подібна до поділу на нуль, що не допустимому для скалярних величин. Якщо детермінант не дорівнює нулю, знайдіть матрицю, зворотну матриці-знаменника. Найбільш поширені способи знаходження оберненої матриці - метод Гаусса-Жордана і процедура знаходження матриці алгебраїчних доповнень. Перевірте, чи правильно ви знайшли зворотну матрицю. Помножте зворотну матрицю на пряму, в результаті ви повинні отримати одиничну матрицю. Одинична матриця - це така, все елементи якої дорівнюють нулю, крім діагональних, які дорівнюють одиниці.
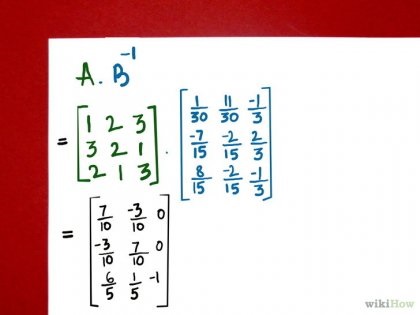
Помножте матрицю-чисельник на зворотну знаменника матрицю. Врахуйте, що, на відміну від множення скалярних величин, в даному випадку порядок множників має значення. При множенні чисел 2, помножене на 4 дає той же результат, що і 4, помножене на 2. У векторній математики множення матриці-чисельника на зворотну знаменника матрицю дає результат, відмінний від того, якби зворотна матриця була помножена на матрицю-чисельник.
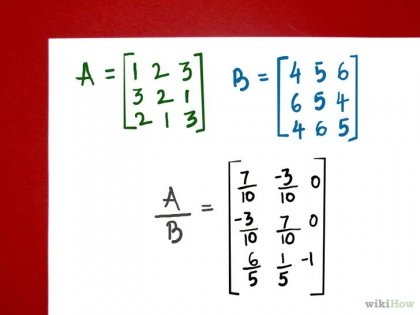
Зауважте, що результат множення матриць відповідає шуканого. Матриця, що не визначена строго в матричної алгебри, обчислюється шляхом знаходження оберненої матриці та множення на неї ділимо матриці.
254310 254311 254312