Щоб приступити до виконання лабораторної роботи, попередньо потрібно отримати у викладача допуск, для чого необхідно в позаурочний час:
Уважно прочитати методичні вказівки до роботи.
Вивчити теоретичний матеріал, необхідний для засвоєння знань по роботі. При необхідності вивчити додаткову літературу (список літературних джерел додається).
При підготовці до заняття ознайомитися з лабораторної установкою, з'ясувати для себе, що і як вимірювати.
Під час аудиторного лабораторного заняття отримати допуск до роботи у викладача.
Як оформити лабораторну роботу
Титульний лист: Міністерство освіти і науки РК, ЮКГУ ім. М.Ауезова, кафедра «Фізика», назва і номер лабораторної роботи, ПІБ студента, група, ПІБ викладача, місто, рік.
Ксерокс, сканування тексту методичних вказівок не допускаються.
Якщо в роботі потрібно будувати графіки, то їх необхідно креслити на міліметрівці.
Захист і оцінка виконаної лабораторної роботи
Щоб захистити виконану лабораторну роботу, потрібно представити викладачеві письмовий і усний звіт по роботі. Максимальний бал (див. Сіллабус) за лабораторну роботу виставляється студенту, якщо:
Студент виконав роботу в повному обсязі.
Студент знає обладнання, технічні та інструментальні засоби, що використовуються в роботі, а також на лабораторній установці може показати, як він виконував роботу, що і як вимірював.
Студент дає повні і правильні відповіді на контрольні питання.
Мінімальний бал (див. Сіллабус) за лабораторну роботу виставляється студенту, якщо він виконав роботу в повному обсязі, правильно її оформив, але під час захисту надав тільки письмовий звіт.
Лабораторна робота № 1. Математична обробка результатів прямих вимірювань
Цілі і завдання роботи: ознайомлення з методикою обробки результатів багаторазових прямих вимірювань на прикладі обробки даних вимірювань періоду коливань математичного маятника, визначення найбільш вірогідного значення вимірюваної величини, стандартного відхилення, довірчого інтервалу при заданій надежності
Будь-яке вимірювання через недосконалість органів почуттів людини і вимірювальних приладів сопряжно з похибками. При будь-яких вимірах допускаються деякі помилки, тому результати вимірювань дають нам не справжнє, а лише наближене значення вимірюваної велічіни Встановлення похибки вимірювання, інтервалу, в якому лежить істинне значення вимірюваної величини, є необхідною умовою надійності експерімента Похибки вимірювань ділять на промахи, а також систематичні і випадкові погрешності
Промахи виникають внаслідок несправності приладу або неуважності спостерігача, при порушенні методики експерименту або умов його проведенія У більшості випадків промахи добре помітні, так як соответствущего їм відліки різко відрізняються від подібних отсчетов Результат вимірювання, що містить промах, не повинен враховуватися при обробці даних - його слід просто отбросіть
Систематичні похибки виникають внаслідок несправності або неточності градуювання вимірювальних приладів, при використанні для розрахунків неточних даних, а також внаслідок недосконалості самого методу ізмеренія Ці помилки впливають на результати вимірювання завжди односторонне Очевидно, що вплив систематичних помилок можна знизити збільшенням числа ізмереній Однак, якщо природа і характер систематичних помилок відомі, вплив їх на результат вимірювання можна врахувати введенням поправок і виключити.
Випадкові помилки обумовлені флуктуаціями вимірюваної величини, поява їх не може бути попереджено, тому вони можуть зробити певний вплив на окремі вимірювання, змінюючи результат в обидві сторони, тобто і збільшувати і зменшувати іх Вони підпорядковуються статистичним законам, тому вплив випадкових помилок на результат вимірювань можна врахувати або значно уменьшіть Застосовуючи закони теорії ймовірності, визначаються найбільш імовірні значення вимірюваних величин і можливі відхилення від цих значень.
Нехай при багаторазовому вимірі деякої фізичної величини

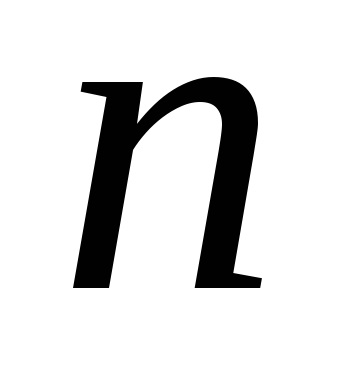
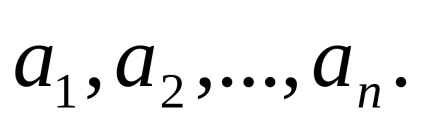
Кожне окреме вимір відрізняються від середнього арифметичного

відхилення
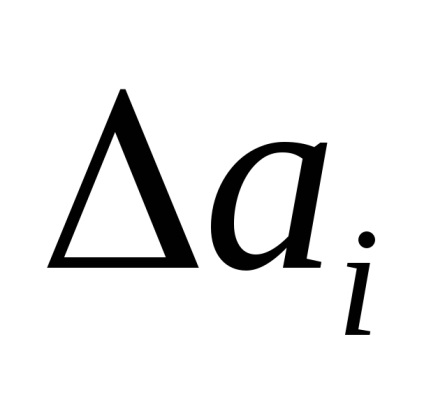
З досвіду відомо: чим більше помилка, тим імовірність її прояви меньше Крім того, якщо число вимірювань дуже велике, то помилки, однакові за величиною, але різні за знаком, зустрічаються однаково часто Швидкість зменшення ймовірності появи похибки
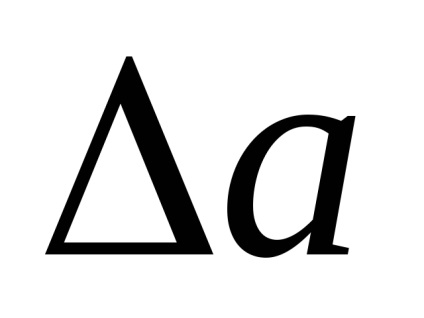
Чим менше дисперсія, тим менше ймовірність появи більшої за величиною випадкової помилки і менше розкид окремих значеній
Корінь квадратний з дисперсії вимірювань називається середньої квадратичної помилкою
якщо замість
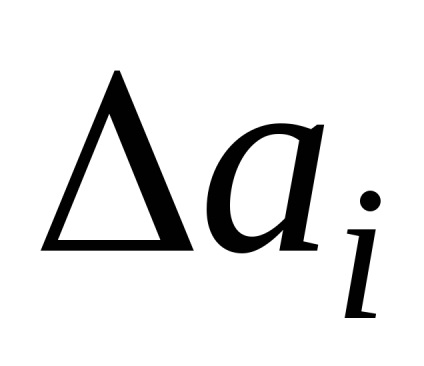
У вираз (1.1.7) входить величина

оцінки дисперсії
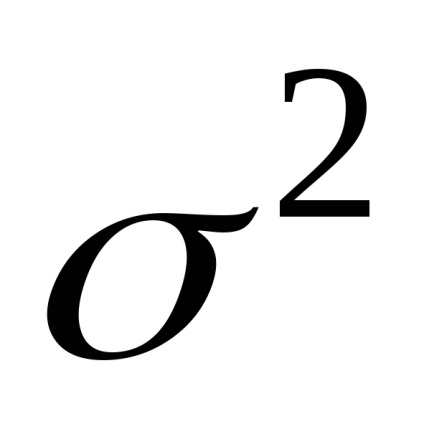
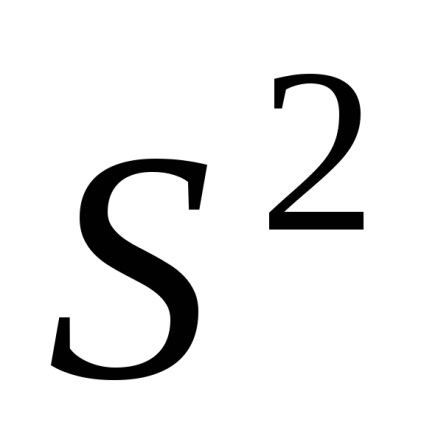
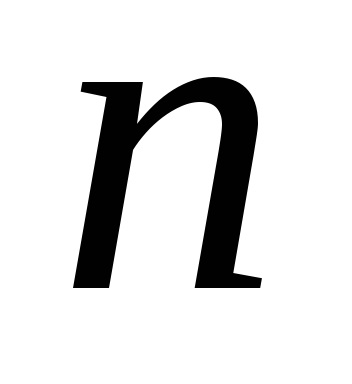
Завдання обробки вимірювань полягає в визначень інтервалу від
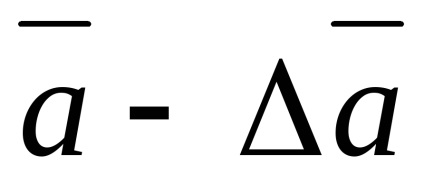

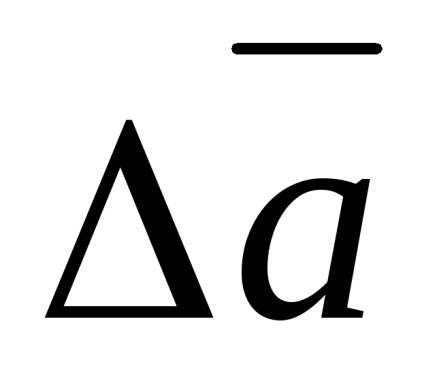

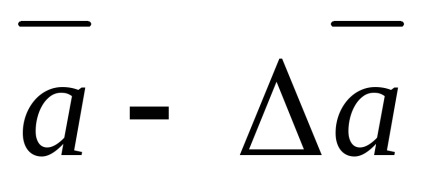
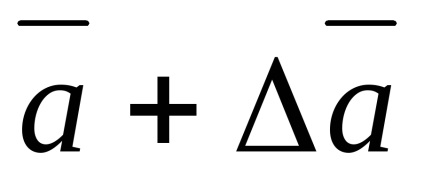

Якщо число вимірювань досить велике, то довірча ймовірність висловлює частку із загального числа вимірів, в яких вимірюється величина виявляється в межах довірчого інтервала Наприклад, якщо зроблено 100 вимірювань, то при довірчій ймовірності
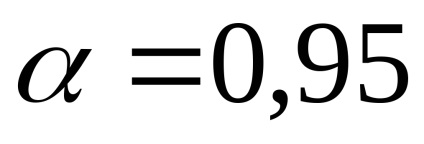
З теорії помилок слід, що при великій кількості вимірів (більше ста дослідів) довірча ймовірність інтервалу від
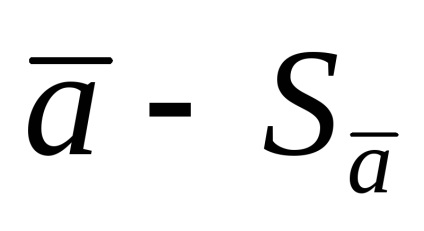
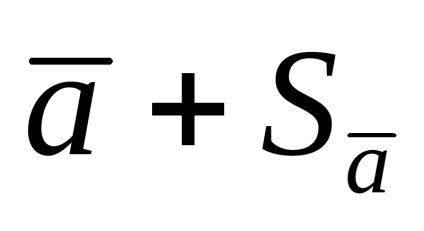
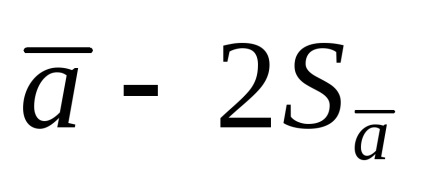
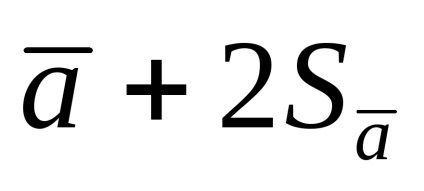
У тих випадках, коли число вимірів невелика, відсутні умови для суворого прояви статистичних закономірностей, які лежать в основі визначення випадкових погрешностей Це призводить до того, що значення середньоквадратичного відхилення від середнього Sa. обчислене за формулою (1.1.9), неточно, і неточність тим більше, чим менше число вимірювань.
Отже, щоб гаранатіровать, що істинне значення вимірюваної величини із заданою вірогідністю знаходиться в межах довірчого інтервалу, останній доводиться увелічівать При обмеженому числі вимірювань за межу довірчого інтервалу приймається не Sa. а таке значення:
чисельне значення
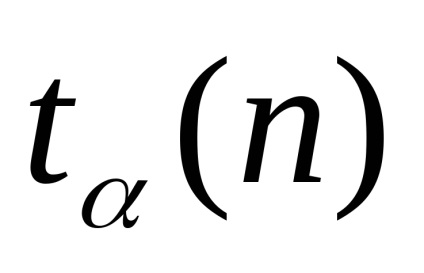
Результати ізмереніяй різнорідних величин не можна порівнювати один з одним по їх абсолютним ошібкам Для порівняння точності вимірювань таких величин вводиться відносна помилка - відношення абсолютної помилки до середнього значення вимірюваної велічіни
За відносної похибки зручно порівнювати результати вимірювань однорідних велічін
Устаткування: математичний маятник, секундомір.
Порядок виконання роботи:
Виміряти час 20-30 коливань маятника (кількість коливань маятника N задається викладачем) Вимірювання повторити n разів (кількість дослідів n задається викладачем)
Для кожного досвіду знайти період коливань маятника за формулою:
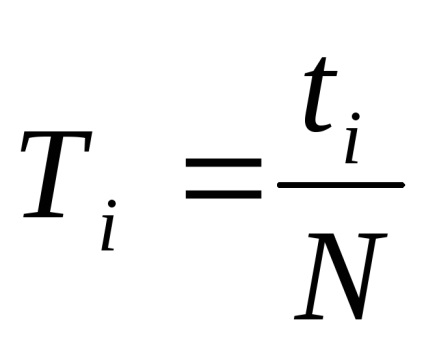
Визначити середнє арифметичне значення періоду коливань маятника за формулою:
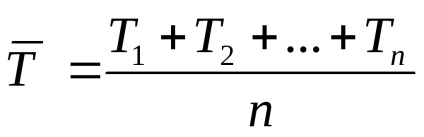
Знайти для кожного досвіду величину
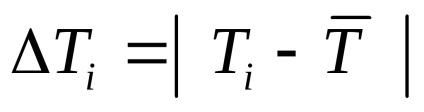
звести
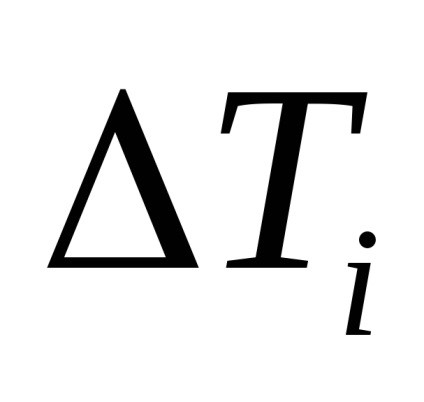
Знайти стандартне відхилення періоду коливань за формулою:
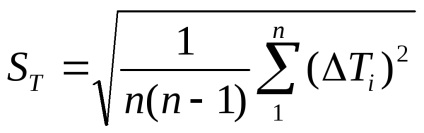
По таблиці, наявної в лабораторії, знайти значення коефіцієнта Стьюдента, відповідне надійності, зазначеної викладачем, і числу дослідів.
Вчісле абсолютну помилку вимірювань за формулою:
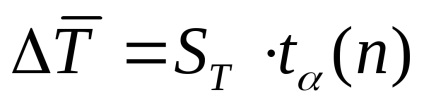
Розрахувати відносну помилку по формулі
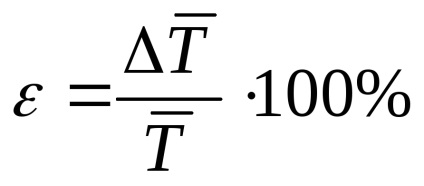
Результати вимірювань і обчислень занести в таблицю: