Перший (ваш) варіант отриманий паралельним переносом.
Другий (мій) варіант отриманий осьової симетрією з використанням паралельного перенесення.
Третім принципово відмінним від інших рішенням повинен бути, мабуть, відповідь з використанням центральної симетрії (без використання осьової), але мені нічого подібного знайти поки не вдалося.
Якщо я вас правильно зрозумів, то ви зараховується варіант "одним відрізком з (2; 2) в (5; 1)", який, однак же, не відповідає поставленому умові (площі може і рівні, але отримані фігури за допомогою обертань і переворотів неможливо накласти один на одного, тобто вони різної форми). Так що, якщо цей варіант вас з якоїсь причини влаштовує, то у мене все 3; якщо ж ні, то я не уявляю, звідки можна взяти третій принципово відмінний.
Mefody, я сумніваюся що крім зазначеного першого способу існують рішення де і форма і площа збігаються. Та й не ясно що означає принципово інше рішення. Але якщо говорити тільки про площу, то я бачу три рішення, але моє друге рішення принципово не відрізняється від рішення Rafaila
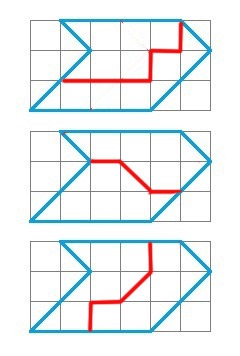
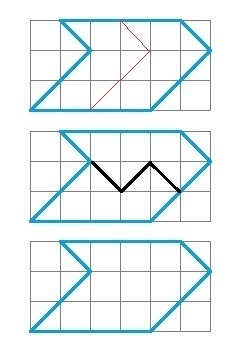
Дозволю собі навести малюнок до відповіді Rafaila
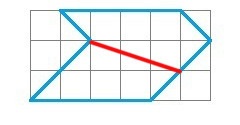
У його рішенні квадратики розбиваються не по полам, а розподіл вироблено однією лінією. А це більш граціозно з точки зору математики.
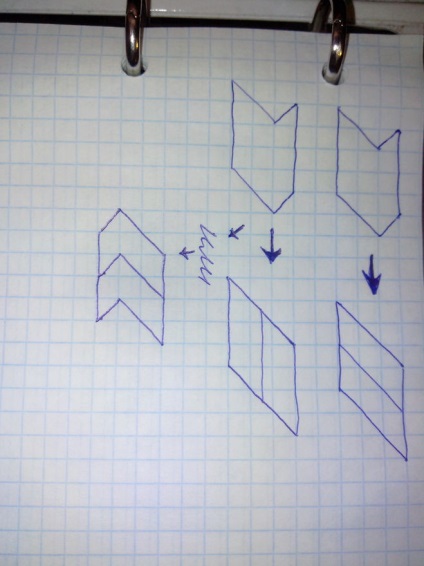
Добрий час доби!
Я не супер математик, але запропоную свою версію відповіді:
Так як в питанні не сказано, що фігуру можна змінювати, я вирішив Вам запропонувати змінити фігуру, але при цьому зберегти площу. І я намалював два варіанти і при цьому в другому варіанті домалював і такий варіант як просто можна перевернути фігуру і поділити вже з низу в верх або з верху вниз.
Прошу вибачення якщо намалював криво, прошу сильно не судити. Дякую всім і бажаю щастя і успіхів в своїх відповідях.