Зграя з 9 злодіїв вкрала золотий злиток.
Під час розподілу видобутку виникли проблеми, і двоє наставили один на одного пістолети.
Чи виживе хтось із них, помруть вони обоє або обидва залишаться жити, невідомо.
А поки вони з'ясовують стосунки, інші вирішили продовжити паювання.
На яку мінімальну кількість шматків потрібно розділити золотий злиток, щоб при будь-якому розкладі все отримали порівну?
Простіше кажучи, потрібно розділити злиток на таку мінімальну кількість шматків, щоб їх можна було роздати порівну одночасно на 7, або на 8, або на 9 осіб, в залежності від результату дуелі.
Шматки можуть бути будь-якої форми, головне - щоб вага кожної частки був однаковим.
І ще. Я знаю, що 22 шматка - це неправильна відповідь, можна ще краще.
Як вирішити цю задачу?
Давайте уявимо злиток у вигляді 504 часток. Тоді при розпилі буде 3 ситуації:
- 7 купок по 72 частки.
- 8 купок по 63 частки.
- 9 купок по 56 часткою.
Спробуємо знайти оптимальний варіант розпилу. Для цього кожен крок буде виділяти мінімальне число шматків максимального розміру, який допустимо на цьому кроці.
- Виділяємо 7 шматків по 56 часткою (більше розмір не можна, так як при діленні на 9 розмір шматка 56 часткою). У нас залишається:
- Виділяємо 3 шматки по 16 часткою (більше розмір не можна, так як при діленні на 7 розмір шматка 16 часткою). У нас залишається:
Це і буде останнім шматком. Разом 7 + 3 + 1 + 6 + 3 + 1 = 21 шматок.
Розміри шматків: 1/9, 1/9, 1/9, 1/9, 1/9, 1/9, 1/9, 2/63, 2/63, 2/63, 5/168, 1/72 , 1/72, 1/72, 1/72, 1/72, 1/72, 1/252, 1/252, 1/252, 1/504.
- 1) Варіант паювання на 8 злодіїв.
Ділимо злиток на вісім рівних часток і приймемо цю частку дорівнює одиниці. Всім порівну.
- 2) Варіант паювання на 9 злодіїв.
Відокремлюємо від кожної з восьми часткою 1/9 частина. В результаті 8 співучасникам злочину дістається по 1-1 / 9 = 8/9 часткою. Визначаємо. що залишається 9-му - (1/9) * 8 = 8/9. Всім порівну.
- 3) Варіант паювання 7 на злодіїв.
Якщо сімом злочинцям роздати по одній частці 1 = (8/9 + 1/9), то залишається одна зайвою. Ось і розділимо її на 7 частин, тобто по 1/7 отримаємо шість шматочків золота, а останній шматочок буде складатися з 1/9 + 2/63 = 1/7. Шістьом дістанеться по (8/9 + 1/9 + 1/7), сьомого (8/9 + 1/9 + 1/9 + 2/63). Все порівну.
У підсумку отримуємо 8 + 8 + 7 = 22 шматка
Особисто у мене вийшло мінімально розділити тільки на 28 частин.
Спочатку ділимо золото на 9 рівних частин.
Потім беремо одну з цих частин і ділимо її на 8 частин.
Далі беремо 2 нерозділені частини і ділимо кожну на 7 частин.
У нас виходить 6 повних кубиків, один розділений на 8 і 2 розділених на 7 кожен.
Якщо залишається 9 осіб, то 6 осіб отримають по цілому кубику, один отримає кубик, розділений на 8 частин і 2 людини отримають по кубику, розрізаному на 7.
Якщо залишиться 8 осіб, то кожен отримає по одному цілому кубику (2 з яких будуть поділені на 7) і по одній восьмій кубика, розділеного на 8 частин.
Якщо залишиться 7 осіб, то кожен отримає по цілому кубику (один з яких розрізаний на 8) і по 2 шматочки від тих двох кубиків, які розрізані на 7 частин (2 кубика по 7 частин це 14 частин, тобто по 2 частини на кожного людини).
Підсумок: у нас вийшло 28 частин - 6 цілих кубиків + 8 частин кубика + 14 частин з двох кубиків.
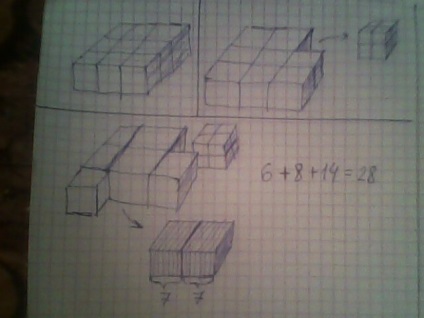
Те ж саме, тільки побільше:
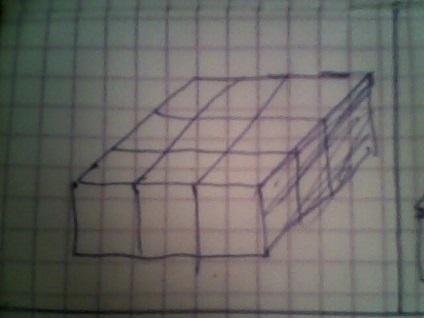
Пропоную наступний варіант решенія.Делім шматок золота на 9 частей.Затем окремо ділимо один такий шматок на 8 частин і 2 інших таких шматка кожен на 7 частей.Получается якщо буде 9 злодіїв то вони отримають кожен по шматку: 6 злодіїв цілі шматки, 2 злодія шматки розрізані на 7 частин і 1 злодій шматок розрізаний на 8 частей.Еслі злодіїв буде 8 то 6 з них отримають по цілому шматку + 1 \ 8 від шматка розрізаного на 8 частин, а 2 злодія отримають по шматку з розрізаних на 7 частин +1 \ 8 від шматка розрізаного на 8 частей.Еслі же злодіїв буде 7 то 6 з них отримає по цілому шматку + по 1 \ 7 від до аждого з 2-ух шматків розрізаних на 7 частин, а 1 злодій отримає шматок розрізаний на 8 частин + по 1 \ 7 від кожного з шматків розрізаних на 7 частей.То є всього буде 8 + 7 + 7 + 1 + 1 + 1 + 1 + 1 + 1 = 28 шматків.
Євген, спасибі, ви мене навели на одну цікаву думку.
Можливо, вдасться отримати менше 22 шматків. але треба ще добре подумати. - 9 місяців тому