
Про біткоіни вже чимало сказано - від загадкової історії його створення до ступеня впливу на світову економіку. У цій статті ми хочемо подивитися на все під іншим кутом, заглибитися в технічні деталі і проаналізувати використовувані математичні методи.
Що таке біткоіни?
У своїй основі біткоіни - це цифровий файл, який зберігає записи про всі транзакції - з моменту виникнення перших кріптомонет до останньої транзакції, в якій вони брали участь. Записи згруповані в блоки, кожен з яких містить інформацію про частину або всіх недавніх транзакціях, не включених до реєстру раніше, а також додаткову службову інформацію.
структура блоку
Кожен блок містить обов'язкові елементи - заголовок і список транзакцій. Тема включає хеш даного блоку, хеш попереднього блоку, хеші транзакцій і додаткову інформацію про блок. Хеш-функція (хешування) - математичне перетворення вихідного масиву даних довільної довжини в унікальну буквено-цифрову рядок фіксованої довжини, яка, по суті, є шифром і ідентифікує вхідний елемент. Рядок не може бути перетворена в зворотному напрямку. Таким чином, з будь-якого унікального набору даних ми можемо отримати хеш-код (хеш, хеш-суму), який також є унікальним.
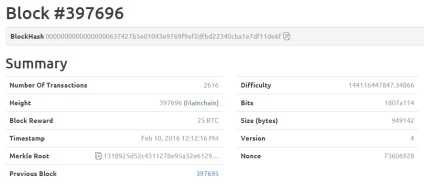
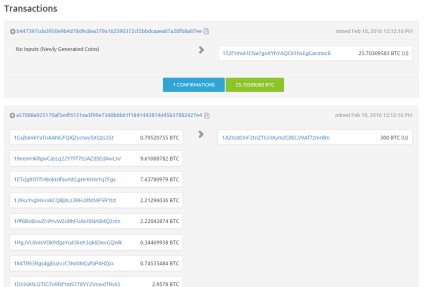
Для того щоб блок потрапив в блокчейн, його потрібно обчислити, тобто знайти пов'язане з ним значення хешу заголовка, менше заданого порогу. Іншими словами, завдання полягає в наступному: підібрати вхідні дані таким чином, щоб хеш починався, наприклад, з 17 нулів. Фактично при цьому відбувається звичайний перебір можливих варіантів хеша. Як тільки вузол знаходить підходящий варіант, він оголошує інших вузлів, що блок обчислений і після перевірки правильності обчислення іншими вузлами, в ході якої відбувається одноразове обчислення хеша, блок потрапляє в блокчейн.
Іноді одночасно вирішується більше одного блоку і виходить кілька гілок. В цьому випадку ланцюг триває після першого отриманого блоку. Інші через особливості передачі блоків від вузла до вузла могли отримати блоки в іншому порядку і могли будувати слідом за своїм першим отриманим блоком. Нічия зникає, коли хтось вирішить наступний блок. За загальним правилом все переходять на найдовшу гілка. Через розрахунків блоки рідко вирішуються одночасно, але ще рідше це трапляється кілька разів поспіль. В результаті блокчейн швидко стабілізується, тобто у всіх однакові блоки у кінця ланцюга.
Той факт, що в кінці ланцюга буває невизначеність має важливе значення для безпеки транзакції. Наприклад. Якщо ваша транзакція виявиться в одній з коротких гілок, вона втратить своє місце в ланцюгу. Зазвичай це означає, що воно просто повернеться в масив непідтверджених транзакцій і потрапить в один з наступних блоків.
Алгоритм цифрового підпису
Відправляючи гроші, ви повідомляєте в мережу суму, на яку зменшиться ваш баланс і виросте баланс одержувача. При цьому діє просте правило: при здійсненні транзакції вхід (що надійшли на ваш гаманець кошти) повинен бути витрачений повністю, тобто щоб відправити суму, яка не дорівнює жодному з входів, потрібно буде відправити на свій рахунок здачу.
Підпис залежить від повідомлення, прикріпленого до перекладу, тобто вона нова для кожної транзакції, тому використовувати її для іншої транзакції не вийде. Ця залежність від повідомлення означає також, що його ніхто не зможе змінити, передаючи по мережі, оскільки зміни в повідомленні зроблять недійсною підпис. Сам алгоритм обчислень досить складний. Для підтвердження даних біткоіни використовує алгоритм цифрового підпису на еліптичній кривій (ECDSA) і односторонню функцію з потайним входом. Характерною особливістю останньої є те, що її можна легко обчислити в одному напрямку, але важко вирахувати в зворотному без спеціальної інформації, яку часто ще називають «потайним входом».
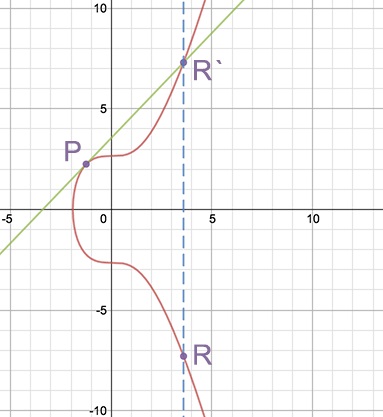
Алгоритм цифрового підпису ECDSA, що використовує еліптичні криві і кінцеві поля, докладно описаний у статті «The Math Behind Bitcoin». З точки зору математики, еліптична крива являє собою рівняння виду: y² = x³ + ах + b. У випадку з біткоіни а = 0 і b = 7, і крива виглядає наступним чином:
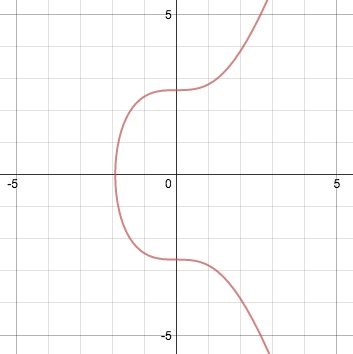
Еліптичні криві мають кілька відмінних рис. Наприклад, невертикальною пряма, яка перетинає криву в двох точках, перетне її в третій точці, що лежить на кривій. Ще однією властивістю є те, що якщо невертикальною пряма стосується еліптичної кривої в одній точці, то вона неодмінно перетне криву ще рівно в одній точці. Знаючи два цих властивості, ми можемо провести операцію складання або подвоєння точок, складових криву.
Для складання точок P і Q, ми проводимо через них пряму, яка перетне криву в деякій точці R '. Потім знаходимо на кривій точку R, симетричну R 'щодо осі X. Вона і буде сумою точок P і Q.
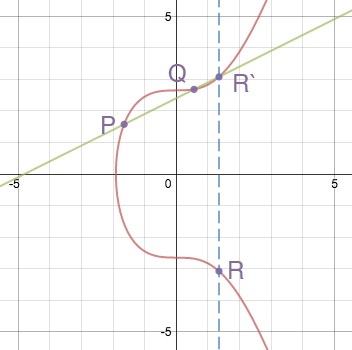
При подвоєнні точки, P + P = R, ми проводимо пряму, яка стосується кривої в точці P. Згідно властивостями кривої, пряма перетне її ще в одній точці - R '. Точка R, симетрична R 'щодо осі X і буде результатом подвоєння P.
Дві ці величини можна використовувати для визначення скалярного твори, R = aP, яка визначається як додавання точки Р самої до себе a раз. Процес скалярного множення спрощується за рахунок поєднання процесів складання і подвоєння точок. Наприклад, семиразове додавання точки P, R = 7P = P + (P + (P + (P + (P + (P + P))))), можна представити у вигляді: R = P + 2 (Р + 2P) . Тобто замість 7 операцій ми отримали всього 4 - 2 операції подвоєння і 2 складання.
Інше поняття, яке використовує алгоритм ECDSA, це кінцеве поле. Його можна розглядати як заданий діапазон позитивних чисел, в рамках якого здійснюються всі операції. Поєднуючи два поняття - еліптична крива і кінцеве поле, ми отримаємо функцію, яка за своїм зовнішнім виглядом не матиме нічого спільного з колишньою кривої, але рівняння і властивості її залишаться колишніми. Наприклад, еліптична крива біткоіни, y² = x³ + 7, певна на кінцевому полі по модулю 67, буде виглядати наступним чином:
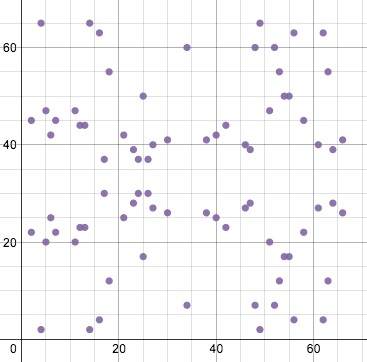
При цьому симетрія точок щодо осі X зберігається. Просто тепер це безліч точок, в яких все х і у значення є цілими між 0 і 66. Візуально буде відрізнятися і процес складання і подвоєння точок. Тепер прямі обмежені кінцевим діапазоном і будуть обертатися «навколо поля» - лінія досягає краю, в нашому прикладі 67, і триває з іншого його кінця, зберігши колишній нахил, але зі зрушенням. Тому, складання точок (2, 22) і (6, 25) в даному випадку виглядає так:
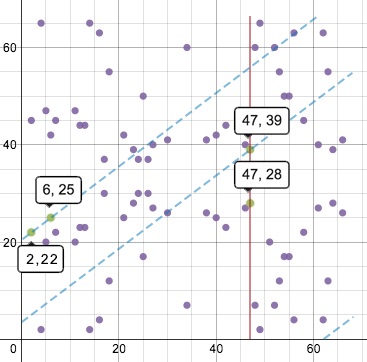
Пряма проходить через 2 зазначені точки, потім впирається в край поля і, продовжуючи, перетинає точку (47, 39). Симетрична їй «щодо осі X» буде точка (47, 28), яка і є результатом складання.
Для того щоб застосувати алгоритм ECDSA в мережі біткоіни, ми повинні мати фіксований набір параметрів еліптичної кривої і її кінцевого поля, єдиний для всіх користувачів. Інакше кожен буде вирішувати свої власні рівняння, які не збігатимуться один з одним. До фіксованим параметрами відносяться рівняння кривої, значення модуля поля, базова точка, що лежить на кривій, і порядок базової точки, тобто скільки разів вона може бути додана до себе до моменту, коли її дотична не стане вертикальною. Для всіх цих параметрів біткоіни використовує величезні числа. Так алгоритм дозволяє забезпечити безпеку, виключаючи можливість випадкового підбору даних. У разі біткоіни ці значення такі (наведені в шістнадцятковому вигляді):
Рівняння еліптичної кривої: y² = x³ + 7.
Простий модуль = 2256 - 232 - 29 - 28 - 27 - 26 - 24 - 1 = FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE FFFFFC2F.
Базова точка = 04 79BE667E F9DCBBAC 55A06295 CE870B07 029BFCDB 2DCE28D9 59F2815B 16F81798 483ADA77 26A3C465 5DA4FBFC 0E1108A8 FD17B448 A6855419 9C47D08F FB10D4B8.
Порядок = FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE BAAEDCE6 AF48A03B BFD25E8C D0364141.
Дана конкретна реалізація ECDSA відома як secp256k1 і є частиною сімейства стандартів, пропонованих для використання в криптографії.
Облік балансу коштів
На відміну від грошей, посилаючи біткоіни, ви швидше за кладете їх в загальнодоступну осередок з математичною задачею, яка відкриє дверцята. І хоча зазвичай розв'язати цю проблему може тільки один власник публічного ключа, можливі і більш складні умови. Наприклад, для escrow-транзакції може знадобитися 2 з 3 можливих підписів. Інший приклад - це найперша біткоіни-транзакція в історії. Це завдання міг вирішити будь-який користувач.
На що можна витратити?
Шопінг. В першу чергу біткоіни - це засіб платежу. В даний час криптовалюта до оплати приймають велику кількість стартапів і великих компаній, таких як Microsoft, Overstock, Dell, TigerDirect і ін. За біткоіни ви можете придбати практично будь-які фізичні товари, послуги або цифровий контент, як в інтернеті, на численних сайтах, так і в ряді офлайнових точок - кафе, магазинах, АРТСТУДІО і т.д. На сьогоднішній день в світі існує більше 7,5 тис. Центрів прийому біткоіни. Побачити їх можна на мапі.
Обміняти на іншу валюту. Незважаючи на все різноманіття торгових пропозицій, говорити про повсюдне визнання біткоіни, особливо в Росії, ще рано. Якщо в обраному вами магазині криптовалюта не приймається, ви можете обміняти її на готівку або на іншу електронну валюту. Зробити це можна, наприклад, в обмінному пункті xmlgold.eu. що пропонує близько 40 напрямків обміну біткоіни. Серед доступних варіантів - висновок в інші платіжні системи (AdvCash, OKPAY, Perfect Money, Payeer і інші), миттєвий банківський переказ, за допомогою якого можна оплатити покупку або отримати готівку, а також висновок на карти Visa і MasterCard в доларах або євро по всьому світу.
Відправитися в подорож. Замовити квитки на літак, забронювати номер в готелі, оплатити туристичний тур - все це можна зробити за допомогою біткоіни. Сьогодні існує кілька великих туристичних сервісів, що приймають криптовалюта в якості оплати, один з них - BTCTrip. Інтерфейс цього ресурсу не відрізняється від інших порталів, присвячених подорожам, але оплатити поїздку можна біткоіни. У самому подорожі ви також зможете використовувати кріптомонети, і вам не знадобиться шукати обмінні пункти, як у випадку зі звичайною валютою, адже в більшості зарубіжних країн продавці охоче приймають криптовалюта, в тому числі завдяки різним сервісам оплати, таким як Blade. Circle. Plutus.
Направити на благодійність. Можливість відправляти як великі суми, так і здійснювати мікроплатежі, а також низькі комісії на обробку транзакції роблять біткоіни ідеальним інструментом для відправки коштів на благодійність. Однією з перших можливість робити пожертви в BTC надала організація BitGive Foundation, яка займає збором коштів для Червоного Хреста, Water Project, Save the Children і інших програм. Пожертвування в криптовалюта приймає міжнародна екологічна організація Greenpeace. Не так давно була запущена програма Bitcoin Charity 2.0, яка дозволяє спрямувати кошти безпосередньо нужденним. Проект забезпечує повну прозорість за рахунок використання технології блокчейн.
Надіслати міжнародний грошовий переказ. Біткоіни дозволяє відправити будь-яку суму майже в будь-який куточок світу. При цьому комісії на обробку транзакцій, як уже зазначалося, мінімальні. Крім того, відправка коштів в біткоіни відбувається значно швидше звичайних банківських переказів, що робить криптовалюта одним з найбільш зручних платіжних інструментів. Для ще більшого комфорту користувачів розробники випускають різні сервіси, що спрощують відправлення переказу. Наприклад, Bitwage - міжнародний зарплатний сервіс, BitPesa - сервіс для міжнародних грошових переказів в країни Африки, і інші подібні ресурси.