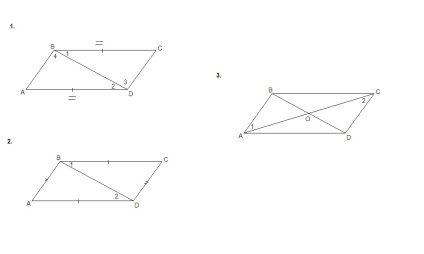
1 ознака.
Якщо в чотирикутнику дві сторони рівні і паралельні, то цей чотирикутник - паралелограм.
Дано: ABCD, AD║ BC, AD = BC.
Довести: ABCD - паралелограм.
Доведення:
Проведемо BD.
ВС = AD по умові,
∠1 = ∠2 як навхрест лежачі при перетині AD║BC січною BD,
BD - загальна сторона для трикутників ABD і CDB, ⇒
ΔABD = ΔCDB по двох сторонах і куту між ними.
З рівності трикутників випливає, що
∠3 = ∠4, а це навхрест лежачі кути при перетині прямих CD і АВ січною BD, значить
CD║AB.
Якщо в чотирикутнику протилежні сторони паралельні, то це паралелограм.
2 ознака.
Якщо в чотирикутнику протилежні сторони рівні, то цей чотирикутник - паралелограм.
Дано: ABCD, AB = CD, BC = AD.
Довести: ABCD - паралелограм.
Доведення:
Проведемо BD.
ВС = AD по умові,
AB = CD за умовою,
BD - загальна сторона для трикутників ABD і CDB, ⇒
ΔABD = ΔCDB за трьома сторонами.
З рівності трикутників випливає, що
∠1 = ∠2, а це навхрест лежачі кути при перетині прямих ВС і AD січною BD, значить ВС║AD і ABCD - паралелограм за першою ознакою.
3 ознака.
Якщо в чотирикутнику діагоналі точкою перетину діляться навпіл, то цей чотирикутник - паралелограм.
Дано: ABCD, AC∩BD = O, AO = OC, BO = OD.
Довести: ABCD - паралелограм.
Доведення:
AO = OC за умовою,
BO = OD за умовою,
∠АОВ = ∠COD як вертикальні, ⇒
ΔАОВ = ΔCOD по двох сторонах і куту між ними.
Значить, AB = CD і ∠1 = ∠2, а це навхрест лежачі кути при перетині прямих АВ і CD січною АС, значить АВ║CD.
ABCD - паралелограм за першою ознакою.