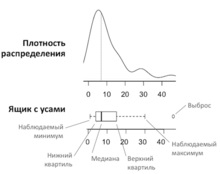
Графік 2. Порівняння щільності розподілу і Ящика з вусами
Ящик з вусами. діаграма розмаху (англ. box-and-whiskers diagram or plot, box plot) - графік, який використовується в описовій статистикою, компактно зображає одномірний розподіл ймовірностей.
Такий вид діаграми в зручній формі показує медіану (або, якщо потрібно, середнє), нижній і верхній квартили, мінімальне і максимальне значення вибірки і викиди. Кілька таких ящиків можна намалювати пліч-о-пліч, щоб візуально порівнювати одне розподіл з іншим; їх можна розташовувати як горизонтально, так і вертикально. Відстані між різними частинами ящика дозволяють визначити ступінь розкиду (дисперсії) і асиметрії даних і виявити викиди.
Компактність подання інформації
Графік «ящик з вусами», або «ящічковая діаграма», був розроблений Джоном Тьюки в 1970-х роках. По суті, ящик з вусами - це швидкий спосіб вивчення одного або декількох наборів даних в графічному вигляді. Цей графік може здатися більш примітивним, ніж, наприклад, гістограми. але він має деякі переваги. Він займає менше місця і тому особливо корисний для порівняння розподілів між декількома групами або наборами даних. Крім того, ящик з вусами у своїй первісній формі простий для побудови.
Якщо на третьому графіку, де показані щільності розподілу, не можна толком нічого розглянути і порівняти, то на четвертому графіку, що відображає ящики з вусами, легко можна оцінити медіани, квартили, міру варіабельність (дисперсії) і асиметрію в даних, а також виявити викиди. Асиметрію даних можна побачити не тільки по медіані, зміщеною до якогось кінця ящика, а й по різній довжині вусів, що виходять з ящика.
Графік «ящик з вусами» дуже простий для розуміння і саме тому часто використовується в різних публікаціях для візуалізації даних.
Межами ящика служать перший і третій квартили (25-й і 75-й процентилі відповідно), лінія в середині ящика - медіана (50-й процентиль). Кінці вусів - краю статистично значущою вибірки (без викидів), і вони можуть визначатися декількома способами. Найбільш поширені значення, що визначають довжину «вусів»:
- Мінімальна і максимальна спостережувані значення даних по вибірці (в цьому випадку викиди відсутні);
- Різниця першого квартиля і півтора межквартільних відстаней; сума третього квартиля і півтора межквартільних відстаней. У загальному вигляді ця формула має вигляд
де X 1> - нижня межа вуса, X 2> - верхня межа вуса, Q 1> - перший квартиль, Q 3> - третій квартиль, k - коефіцієнт, найбільш часто вживане значення якого дорівнює 1,5.
- Середнє арифметичне за вибіркою ± одне стандартне відхилення; [Джерело не вказано 1134 дня]
- 9-й і 91-й процентилі;
- 2-й і 98-й процентилі.
Дані, що виходять за межі вусів (викиди), відображаються на графіку у вигляді точок, маленьких гуртків або зірочок. Іноді на графіку відзначають середнє арифметичне і його довірчий інтервал ( «зарубка» на ящику). Іноді зарубками позначають довірчий інтервал для медіани.
У зв'язку з тим, що не існує єдиного загального згоди щодо того, як саме будувати «ящик з вусами», побачивши такого графіка необхідно шукати інформацію в супровідному тексті щодо того, за якими параметрами ящик з вусами будувався.
Модифікації ящика з вусами
Незважаючи на свою простоту і зручність, первісна форма ящика з вусами володіє і деякими недоліками. Один з таких істотних недоліків - відсутність на графіку інформації про кількість спостережень за вибіркою. Дійсно, ящик з вусами дозволяє порівняти медіани, квартили, мінімуми і максимуми по різним вибірках, але якщо ми захочемо зробити висновок про загальну медіані по всій сукупності вибірок, то ми не зможемо цього зробити, не вдаючись до розрахунків на вихідних даних. У 1978 році первісна форма ящика з вусами були внесені зміни МакГілл, Ларсеном і Тьюки. Вони запропонували враховувати розмір вибіркової сукупності, малюючи ящики різного розміру, а також зобразили на графіку довірчий інтервал для медіан у вигляді розбіжних клинів. Чим більше ящик за розмірами, тим більше кількість спостережень у вибірці, по якій будувався цей ящик. Що стосується довірчого інтервалу, то він являє собою виїмки на кожному з ящиків; в разі, якщо отримані виїмки різних ящиків не перетинаються, їх медіани статистично значимо різняться.
Інша модифікація отримала назву «histplot» (скор. Від «histogram plot», з англ. - «графік-гістограма»). Тепер на графіку відображаються щільності розподілу по трьом точкам: медіані, першому і третьому Квартиль. Відповідно, замість прямокутника, «ящик» тепер є дві рівнобедрені трапеції, що мають суміжне підставу.
Подальша зміна отримало назву «vaseplot» (з англ. - «графік-ваза») через візуального подібності «ящика» з вазою. На даному графіку проводиться відображення всіх щільності ймовірностей від першого до третього квартиля. Затемнені області представляють собою довірчий інтервал медіани.