Вивчення дифракції світла від дифракційної решітки
Мета роботи: вивчення дифракційної картини від дифракційної решітки в світлі; визначення постійної дифракційної решітки і довжини хвилі монохроматичного світла.
Прилади й приналежності: робоче місце студента РМС 3, що включає: оптична лава (монтажна плита); джерело світла (лазер); діафрагма зі щілиною (дифракційне перешкода); дифракційна решітка, екран з міліметровою сіткою.
Зустрічаючи на своєму шляху перешкоди, світлові хвилі можуть відхилятися від прямолінійного напрямку поширення в область геометричної тіні. Будь-які відхилення при поширенні хвиль від законів геометричної оптики називаються дифракцией (крім випадку заломлення світла на межі поділу двох середовищ різної оптичної щільності). До дифракції хвиль фактично відносяться всі ефекти, що виникають при взаємодії хвиль з об'єктами будь-яких розмірів, навіть малих порівняно з довжиною дифрагує хвилі .
Велике практичне значення має дифракція світла при падінні його на дифракційну решітку. У найпростішому випадку дифракційна решітка являє собою систему паралельних один одному щілин, розділених непрозорими проміжками рівної ширини.
На рис. 1 показані основні характеристики дифракційної решітки.
Розподіл інтенсивності світла в дифракційної картині визначається інтерференцією вторинних хвиль, що приходять в точку спостереження від різних щілин дифракційної решітки. Найчастіше для спостереження дифракції на дифракційних гратах створюються умови, коли на дифракційну решітку нормально падає плоска хвиля (дифракція Фраунгофера). У цьому випадку спостерігається дифракція в паралельних променях. Відповідно до теорії, така дифракційна картина локалізована на нескінченності, і для її спостереження необхідно використовувати збиральну лінзу.

Ширина кожної щілини дорівнює a. ширина непрозорого проміжку дорівнює b. Величина d a b називається постійної (або періодом) дифракційної решітки. Обидва проміжку - прозорий і непрозорий - утворюють штрих.
На рис. 1 зображений хід паралельних променів до і після дифракційної решітки. Світловий пучок падає нормально до площини дифракційної решітки (ДР). В результаті дифракції світлові промені відхиляються на деякий кут (кут дифракції), збираються лінзою Л. а на екрані Е. розташованому в фокальній площині лінзи Л. утворюється дифракційна картина, що представляє собою систему максимумів і мінімумів світла. При візуальному спостереженні роль лінзи грає кришталик ока.
У напрямку початкового поширення світла буде розташовуватися центральний максимум (або максимум нульового порядку) М0. Максимуми 1-го, 2-го, 3-го і інших вищих порядків (М1. М2. М3 відповідно) розташовуються сіммет-річно щодо максимуму нульового порядку з обох боків від нього. Положення максимумів визначається такими значеннями кутів дифракції k (k 0, 1, 2, 3.), для яких хвилі, що приходять в точку спостереження від усіх щілин підсилюють один одного.
Найбільшою інтенсивністю володіє максимум нульового порядку. Зі збільшенням номера порядку максимуму інтенсивність максимуму слабшає.
У разі нормального падіння світла на решітку положення головних максимумів визначається з умови:
де - кут дифракції, тобто кут між нормаллю до грат і напрямком відхилення променів на решітці; - довжина дифрагує хвилі; k - порядок максимуму (k 0, 1, 2, 3.).
Умова спостереження максимумів формулюється так: максимуми при дифракції плоскої хвилі на дифракційної решітці спостерігаються в тих точках простору, для яких добуток постійної дифракційної решітки на синус кута дифракції одно парному числу довжин півхвиль.
Положення мінімумів визначається з умови
dsin (2k 1)
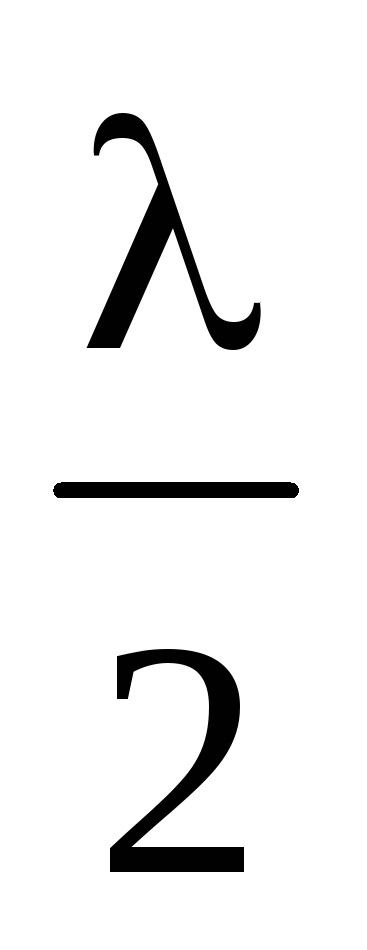
Умова спостереження мінімумів формулюється так: мінімуми при дифракції плоскої хвилі на дифракційної решітці спостерігаються в тих точках простору, для яких добуток постійної дифракційної решітки на синус кута дифракції одно непарному числу довжин півхвиль.
Як випливає з умови (1) кути, під якими спостерігаються світлові максимуми, залежать від довжини хвилі. Таким чином, якщо на дифракційну решітку падає не монохроматичне світло, а світло складного спектрального складу, то після дифракції на решітці на екрані спостерігається спектр, причому фіолетові промені відхиляються гратами на менші кути, ніж червоні (Ф <КР ). В месте расположения нулевого максимума (k 0, 0) находятся нулевые максимумы всех длин волн дифрагирующего света, накладывающиеся друг на друга. При попадании на дифракционную решетку белого света нулевой максимум остается белым (неокрашенным), а по обе стороны от него симметрично относительно нулевого максимума располагаются максимумы более высоких порядков, при этом последовательность их окраски подчиняется условиям (1): фиолетовая часть спектра обращена к центру дифракционной картины, а красная часть − наружу. Это свойство дифракционной решётки можно использовать для исследования спектрального состава падающего света, то есть дифракционная решётка может быть использована как спектральный прибор.
Ширина спектра на екрані залежить від порядку спектра і постійної дифракційної решітки (розтягнутість спектра збільшується зі збільшенням порядку спектра і зменшенням постійної дифракційної решітки).
З геометрії відхилення променя на дифракційної решітці можна розрахувати кут дифракції, рис. 2.
У

де lk відстань між нульовим максимумом і максимумом порядку k; D відстань від площини дифракційної решітки (ДР) до площини екрану (Е).
За умовами експерименту кути k малі (близько 2 ° 3 °), тому можна вважати, що tg k sin k і тоді sin k
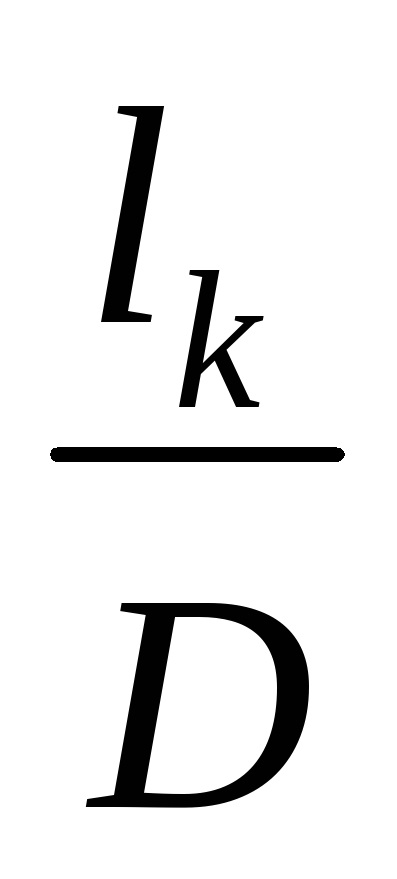
За формулою (2) визначається постійна решітки, дифракцію на якій спостерігали в експерименті.