кінцівка алгоритму

Розгалуження (розбиття множини G на підмножини). покладемо

8. Кінцівка алгоритму. Кінцівка алгоритму випливає з кінцівки безлічі G.

Під методом гілок і меж розуміється алгоритм вирішення задачі, що має деревоподібну структуру пошуку оптимального рішення і використовує результати рішення оціночних завдань. Деревоподібна структура називається зазвичай деревом розгалуження.

Ефективність алгоритму гілок і меж визначається числом вирішених завдань. Рішення завдання складається з двох основних етапів. На першому етапі знаходиться оптимальне рішення (або близьке до нього). На другому етапі проводиться доказ оптимальності отриманого рішення. Другий етап, як правило, виявляється більш трудомістким, ніж перший. Це означає, що число подзадач, що вирішуються до отримання оптимуму, може виявитися значно менше ніж подзадач, що вирішуються для доказу оптимальності.

2. Постановка завдання комівояжера

Класична задача комівояжера (ЗК) формулюється так: є повний зважений орієнтований граф без петель G з безліччю вершин N =; ваги всіх дуг невід'ємні; в цьому графі потрібно знайти гамільтонів цикл мінімальної ваги.

Вихідну інформацію по ЗК вважаємо представленої у вигляді матриці розміру nxn. S =, де sij - вага дуги (i, j) графа G, i =. j =. i ≠ j; всі елементи головної діагоналі матриці S є нулями.

У типовій інтерпретації вершини 1, 2, ..., n графа G - це міста. Дуги відображають можливі елементарні переходи. Комівояжеру, спочатку знаходиться в місті 1, необхідно обійти всі інші міста, побувавши в кожному з них рівно по одному разу, і потім повернутися в місто 1. Ваги дуг графа трактуються як довжини відповідних елементарних переходів. Потрібно знайти має мінімальну довжину допустимий (тобто задовольняє накладеним вимогам) маршрут комівояжера. З урахуванням інших можливих інтерпретацій, на матрицю S вимога симетричності не накладається, не рахується обов'язковим і виконання нерівності трикутника.

3. Завдання комівояжера методом динамічного програмування

Один з основних алгоритмів розв'язання ЗК заснований на принципі динамічного програмування. При викладі цього алгоритму будемо дотримуватися термінології, що відповідає наведеній типовий інтерпретації завдання.

Нехай i - довільний місто (i # 206; N), а V - будь-яка підмножина міст, що не містить міста 1 і міста i. Через М (i, V) позначимо сукупність шляхів, кожен з яких починається в місті i, завершується в місті 1 і проходить в якості проміжних тільки через міста безлічі V, заходячи в кожен з них рівно по одному разу. Через В (i, V) позначимо довжину найкоротшого шляху безлічі М (i, V). Для розв'язуваної задачі В (i, V) - функція Беллмана. Як очевидно, В (1,) - шукана мінімальна довжина простого (без самоперетинів) замкнутого шляху, що проходить через всі міста.

Якщо V - одноелементні безліч, V =, де j ≠ 1 і j ≠ i, то сукупність М (i, V) складається з єдиного шляху μ = (i, j, 1). Тому

i # 206; N, j # 206; , J ≠ i. (1.1)

Припустимо, що значення функції В (i, V) для всіх i # 206; N \ і всіх можливих k-елементних (k

Рівняння (1.1) - (1.12) - рекурентні співвідношення динамічного програмування для розв'язання задачі комівояжера, вони забезпечують реалізацію зворотного методу Беллмана. Обчислювальна складність завдання дорівнює, де С - довільна константа (С> 0), n - число міст.

Приклад 1.1 Вирішити задачу комівояжера, яка визначається матрицею:

Спочатку, користуючись формулою (1.1), визначаємо значення В (i,):

В (2,) = 5 + 6 = 11; В (3,) = 2 + 2 = 4; В (4,) = 5 + 2 = 7;

В (2,) = 2 + 1 = 3; В (3,) = 1 + 1 = 2; В (4,) = 4 + 6 = 10.

Далі за формулою (1.2) послідовно отримуємо (в лівій частині кожного з нижче записаних рівностей виділені ті значення параметра j, на яких під час підрахунку реалізується зазначений в правій частині (1.2) мінімум):

В (2,) = min [s23 + B (3,); s24 + B (4,)] = min (5 + 2; 2 + 10) = 7;

В (3,) = min [s32 + B (2,<4>); s34 + B (4,<2>)] = Min (2 + 3; 1 + 7) = 5;

В (4,) = min [s42 + B (2,<3>); s43 + B (3,<2>)] = Min (5 + 11, 4 +4) = 8;

= Min (4 +7; 3 +5; 4 + 8) = 8.

Отже, оптимальне значення критерію в розглянутому прикладі дорівнює 8.

Виконані виділення дозволяють визначити оптимальний маршрут. Він наступний:

Для запису співвідношень, за якими реалізується прямий метод Беллмана, введемо нові позначення. Нехай М '(V, i) - сукупність шляхів, кожен з яких починається в місті 1, проходить в якості проміжних тільки через міста підмножини V, заходячи в кожен з них рівно по одному разу, і завершується в місті i; тут, як і раніше, i - довільний місто (i # 206; N), а V - будь-яка підмножина N, що не містить міст 1 і i. Довжину найкоротшого шляху безлічі М '(V, i) позначимо В * (V, i). Як очевидно, В * (, 1) - шукана мінімальна довжина простого (без самоперетинів) замкнутого шляху, що проходить через всі міста. Якщо V - одноелементні безліч, V =, де j ≠ 1 і j ≠ i. то сукупність М '(V, i) складається з єдиного шляху μ = (1, j, i). Тому

Припустимо, що значення функції У * (V, i) для всіх i # 206; N і всіх можливих k-елементних (k

Рівняння (1.3) - (1.4) - рекурентні співвідношення динамічного програмування для вирішення класичної задачі комівояжера, вони забезпечують реалізацію прямого методу Беллмана.

Приклад 1.2 Методом прямого рахунку вирішити задачу комівояжера, яка визначається матрицею:

(Зауважимо, що матриця S в даному прикладі та ж, що і в попередньому).

Спочатку, користуючись формулою (1.3), визначаємо значення В * (, i):

В * (, 3) = 4 + 5 = 9; В * (, 2) = 3 + 2 = 5; В * (, 2) = 4 + 5 = 9;

В * (, 4) = 4 + 2 = 6; В * (, 4) = 3 + 1 = 4; В * (, 3) = 4 + 4 = 8.

Далі за формулою (1.4) послідовно отримуємо (в лівій частині кожного з нижче записаних рівностей виділені ті значення параметра j, на яких під час підрахунку реалізується зазначений в правій частині (1.4) мінімум):

В * (, 4) = min [B * (, 3) + s34; B * (, 2) + s24] = min (9 + 1; 5 + 2) = 7;

В * (, 3) = min [B * (, 4) + s43; B * (, 2) + s23] = min (6 + 4; 9 + 5) = 10;

В * (, 2>) = min [B * (, 4) + s42; B * (, 3) + s32] = min (4 + 5; 8 + 2) = 9;

Отже, оптимальне значення критерію в розглянутому прикладі дорівнює 8.

Виконані виділення дозволяють визначити оптимальний маршрут. Він наступний:

4. Завдання комівояжера методом гілок і меж

Іншим алгоритмом розв'язання задачі комівояжера є метод гілок і меж. По суті, це деяка модифікація повного перебору рішень, оптимізується за рахунок того, що за певними ознаками відсікаються неоптимальні безлічі перебору.

Формально будується дерево варіантів, починаючи від кореня. У корені необхідно дати верхню і нижню оцінки. Далі гілок. Чим менший фрагмент дерева доведеться побудувати, тим успішніше спрацював метод гілок і меж.

Трапляються такі визначення:

Поточний рекорд - найбільша з отриманих в процесі реалізації методу нижніх оцінок.

Вершина називається мертвою, якщо верхня оцінка в ній не перевищує поточного рекорду. Виконувати в ній подальше розгалуження марно.

Термінальної називається вершина, в якій верхня і нижня оцінки збігаються.

Вершина, розгалуження в якій вже виконано, називається закритою.

Вершини, які не є мертвими, термінальними або закритими, називаються відкритими. Подальше розгалуження робимо в них.

Рішення закінчується тоді, коли в нашому дереві варіантів немає відкритих вершин. Оптимальним рішенням буде поточний рекорд.

Верхня оцінка визначається за допомогою «жадібного» алгоритму.

Жадібний алгоритм - алгоритм знаходження найкоротшого відстані методом вибору найкоротшого, ще не обраного ребра, за умови, що воно не утворює циклу з вже обраними ребрами. «Жадібним» цей алгоритм названий тому, що на останніх кроках доводиться жорстоко розплачуватися за жадібність (останнє ребро, як правило, найбільше або близько до нього по довжині).

Стратегія: «йди в найближчий (у який ще не входив) місто». Розглянемо для прикладу мережу на рис. 2, що представляє вузький ромб. Нехай комівояжер стартує з міста 1. Алгоритм «йди ви найближчий місто» виведе його в місто 2, потім 3, потім 4; на останньому кроці доведеться платити за жадібність, повертаючись з довгою діагоналі ромба. В результаті вийде не найкоротший, а довжелезний тур.

Щоб обчислити нижню оцінку, спочатку підсумовуємо мінімальні елементи по рядках і по стовпцях, а потім з отриманих сум вибираємо найбільшу, але треба враховувати конфлікт.

Приклад 2.1 Вирішити методом гілок і меж завдання комівояжера, яка визначається матрицею:

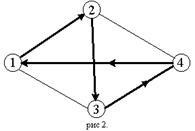
1. Обчислюємо верхню і нижню оцінки в корені:

Верхню оцінку підраховуємо, користуючись, так званим, «жадібним» алгоритмом: кожен перехід робимо з поточного в найближче місто. Отримуємо маршрут:

1 ® 2 ® 4 ® 3 ® 5 ®1

Сумарна вартість даного маршруту дорівнює 12, вона визначає верхню оцінку в корені.

Щоб обчислити нижню оцінку, спочатку підсумовуємо мінімальні елементи по рядках і по стовпцях, а потім з отриманих сум вибираємо найбільшу:

За рядками: 2 + 1 + 2 + 2 + 2 = 9

За стовпцями: 2 + 2 + 3 + 1 + 2 = 10

Вибираємо максимум зі значень і вибираємо 10.

Проаналізуємо стовпці: можемо зрушити на 2 (конфлікт). Звідси нижня межа дорівнює 10 + 2 = 12.

В результаті рішення задачі, далі галузитися нам не куди. Запишемо оптимальний маршрут комівояжера:

Таким чином, задача вирішена.

Практика породжує все нові і нові завдання оптимізації, причому їх складність зростає. Потрібні нові математичні моделі і методи, які враховують наявність багатьох критеріїв, проводять глобальний пошук оптимуму. Іншими словами, життя змушує розвивати математичний апарат оптимізації.

Реальні прикладні завдання дискретної оптимізації дуже складні. Сучасні методи оптимізації далеко не завжди справляються з вирішенням реальних завдань без допомоги людини. Ні, поки такої теорії, яка врахувала б будь-які особливості функцій, що описують постановку задачі. Слід віддавати перевагу таким методам, якими простіше управляти в процесі виконання завдання.

Список використаних джерел

1. Беллмана, Р. Динамічне програмування - М. ІЛ, 1960.- 400 с.

2. Беллмана, Р. Прикладні задачі динамічного програмування - М. Наука, 1965. - 457 с.

4. Р. Беллмана, С. Дрейфус Прикладні задачі динамічного програмування - М. 1965 р 460 стор.

Розгалуження (розбиття множини G на підмножини). покладемо

Інформація про роботу «Метод програмування і схем гілок в процесах рішення задач дискретної оптимізації»

кінцівка алгоритму

Схожі статті