Довжина Маса Час Кут плоский Переміщення точки Швидкість лінійна Швидкість кутова Прискорення лінійне Прискорення кутовий Частота обертання Щільність матеріалу Момент інерції Сила Момент сили, що обертає Робота Кінетична енергія Потужність
Метр Кілограм Секунда Радіан, градус метр метр в секунду Радіан за секунду метр на секунду в квадраті Радіан на секунду в квадраті Оборот в хвилину Кілограм на кубічний метр Кілограм-метр в квадраті Ньютон Ньютон-метр Ньютон-метр Джоуль Джоуль Ватт
м кг з радий, # 945; 0 м м / с рад / с, 1 / c м / с 2 рад / c 2. 1 / c 2 об / хв кг / м 3 кг. м 2 Н (кг. м / с 2) Нм Нм Дж = Нм Дж Вт (Дж / с)
СТРУКТУРА І КЛАСИФІКАЦІЯ МЕХАНІЗМІВ
До складу механізмів входять тверді тіла. які називають ланками. Ланки можуть бути і не твердими (наприклад, ремінь). Рідини і гази в гідро- і пневмомеханізмах ланками не зважають.
Умовне зображення ланок на кінематичних схемах механізмів регламентується ГОСТом. Приклади зображення деяких ланок наведені на рис. 1.1.
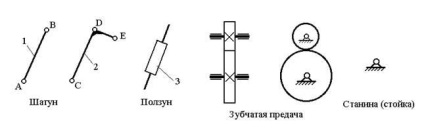
на кінематичних схемах механізмів
- вхідні (провідні) - відмітною ознакою їх є те, що елементарна робота доданих до них сил позитивна (робота сили вважається позитивною, якщо напрямок дії сили збігається з напрямом руху точки її застосування або під гострим кутом до неї);
- вихідні (ведені) - елементарна робота доданих до них сил є негативною (робота сили вважається негативною, якщо напрямок дії сили протилежно напрямку руху точки її застосування);
- нерухомі (станина, стійка).
На кінематичних схемах ланки позначаються арабськими цифрами: 0, 1, 2 і т.д. (Див. Рис. 1.1).
Рухоме з'єднання двох дотичних ланок називається кінематичної парою. Вона допускає можливість руху однієї ланки щодо іншого.
Класифікація кінематичних пар
1. За елементами з'єднання ланок кінематичні пари діляться:
- на вищі (вони є, наприклад, в зубчастих і кулачкових механізмах) - з'єднання ланок один з одним відбувається по лінії або в точці:
- нижчі - з'єднання ланок один з одним відбувається по поверхні. У свою чергу нижчі з'єднання діляться:
2. За кількістю накладених зв'язків. Тіло, перебуваючи в просторі (в декартовій системі координат X, Y, Z) має 6 ступенів свободи. Воно може переміщатися уздовж кожної з трьох осей X, Y і Z. а також обертатися навколо кожної осі (рис. 1.2). Якщо тіло (ланка) утворює з іншим тілом (ланкою) кінематичну пару, то воно втрачає одну або кілька з цих 6 ступенів свободи.
За кількістю втрачених тілом (ланкою) ступенів свободи кінематичні пари ділять на 5 класів. Наприклад, якщо тілами (ланками), що утворили кінематичну пару, втрачено по 5 ступенів свободи кожним, цю пару називають кінематичної парою 5-го класу. Якщо втрачено 4 ступеня свободи - 4-го класу і т.д. Приклади кінематичних пар різних класів наведені на рис. 1.2.
Мал. 1.2. Приклади кінематичних пар різних класів
За структурно-конструктивного ознакою кінематичні пари можна розділити на обертальні, поступальні, сферичні, циліндричні та ін.
Кілька ланок, з'єднаних між собою кінематичними парами, утворюють кінематичну ланцюг.
Кінематичні ланцюги бувають:
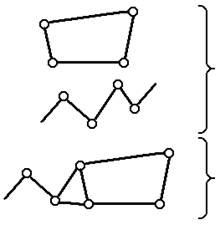
Щоб з кінематичного ланцюга отримати механізм. необхідно:
- одна ланка зробити нерухомим, тобто утворити станину (стійку);
- одному або декільком ланкам задати закон руху (зробити провідними) таким чином, щоб всі інші ланки здійснювали необхідні доцільні руху.
Число ступенів свободи механізму - це число ступенів свободи всій кінематичного ланцюга щодо нерухомого ланки (стійки).
Для просторової кінематичного ланцюга в загальному вигляді умовно позначимо:
кількість рухомих ланок - n,
кількість ступенів свободи всіх цих ланок - 6n,
кількість кінематичних пар 5-го класу - P5,
кількість зв'язків, накладених кінематичними парами 5-го класу на ланки, що входять до них, - 5Р5,
кількість кінематичних пар 4-го класу - Р4,
кількість зв'язків накладених кінематичними парами 4-го класу на ланки, що входять до них, - 4Р4 і т.д.
Ланки кінематичного ланцюга, утворюючи кінематичні пари з іншими ланками, втрачають частину ступенів свободи. Час, що залишився число ступенів свободи кінематичного ланцюга щодо стійки можна обчислити за формулою
Це структурна формула просторової кінематичного ланцюга, або формула Малишева, отримана П.І. Сомовим в 1887 році і розвинена А.П. Малишевим в 1923 році.
Величину W називають ступенем рухливості механізму (якщо з кінематичного ланцюга утворений механізм).
Для плоскої кінематичного ланцюга і відповідно для плоского механізму
Цю формулу називають формулою П.Л. Чебишева (1869). Вона може бути отримана з формули Малишева за умови, що на площині тіло володіє не шістьма, а трьома ступенями свободи:
Величина W показує, скільки повинно бути у механізму провідних ланок (якщо W = 1 - одне, W = 2 - два провідних ланки і т.д.).