Представлені на рис. 24.2 заокруглення традиційної траси аце-мобільних доріг є «жорсткими» типами заокруглень, оскільки при заданих величинах кута повороту 0 і радіусу До отримують единст-дарське становище траси на місцевості, змінити яке можна тільки змінивши відповідно кут або радіус.
На сучасному етапі до траси автомобільних доріг пред'являється ряд обов'язкових вимог (забезпечення зорової плавності і яс-ності, гармонійне вписування полотна дороги в навколишній ланд-шафт, забезпечення найкращих рівнів зручності та безпеки руху-ня), реалізація яких методами традиційного трасування прак-тично неможлива .
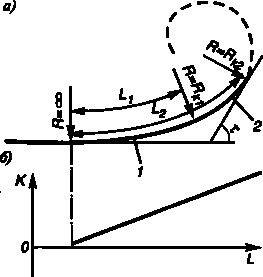
Тому-під час проектування авто-мобільних доріг як в РФ, так і за рубе-жом стали широко застосовувати як само-самостійні елементи траси перехід-ні криві типу клотоїди, лінійний за-кон зміни кривизни якої по її довжині найкращим чином відповідає ус-ловіям руху по ній автомобілів з постійними швидкостями. У параметрах-зації вигляді рівняння клотоїди має вигляд (рис. 24.10):
Мал. 24.10. Зміна кривизни по довжині клотоїди: а - схема клотоїди: 1 - клотоїда; 2 - відрізок клотоїди; б - діаграма кривизни
де А - параметр клотоїди, м; К - радіус клотоїди в точці на відстані Ь від її початку.
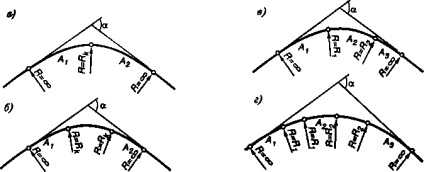
Рис 24.11. Типи заокруглень клотоідной траси:
а - біклотоіда; б - бнклотоіда з круговою вставкою; в - коробова (складова) клотоїда; г - комбіноване закруглення
Радіус кривизни клотоїди змінюється за лінійним законом від К = «> при Ь = О до К = 0 при Ь = оо. Теоретично клотоїди для використання її як елемента траси автомобільної дороги можна обірвати в будь-який її точці, при цьому клотоїда завдовжки Ь = Ь \ матиме радіус в кінцевій точці К = Як. а клотоїда завдовжки Ь = Ь2 буде мати радіус в кінцевій точці К = К ^ причому Кк \> К. Частина перехідної кривої, що лежить між точками ДК 1 і /? к2, також можна використовувати як самостійний еле-мент трасування, це - відрізок клотоїди (див. рис. 24.10).
Клотоідной трасою автомобільної дороги називають трасу, пред-поставлену сполученими між собою в точках з однаковою крівіз-ної, порівнянними по довжині самостійними елементами: клотоїда-ми, відрізками клотоїд, круговими кривими і прямими.
Точки сполучення окремих елементів траси між собою називаючи-ють головними точками траси.
У порівнянні зі звичайною трасою для клотоідной характерно нали-чие більшого числа типів заокруглень (рис. 24.11):
біклотоіда з круговою вставкою (симетрична при А \ = А2 \ несім-метричних при А \ * А2) (рис. 24.11, б);
коробова або складова клотоїда (рис. 24.11, в);
комбіноване закруглення (рис. 24.11, г).
У порівнянні з «жорсткими» закругленнями традиційної траси за-кругления клотоідной траси є виключно «гнучкими», по-кільки при одних і тих же значеннях кута повороту 9 і радіусу До в точ-ках сполучення, змінюючи співвідношення параметрів А суміжних клотоїд
можна деформувати закруглення в плані, найкращим чином приспо-саблівая його до ситуаційних особ-ності і рельєфу місцевості.
Однак слід мати на увазі, що
біклотоіду і Коробова клотоїди
Ріс.24.12. Подання доцільно використовувати лише