Коефіцієнт взаємної спряженості Пірсона С також є мірою зв'язку двох ознак, якщо один з них виміряно за шкалою найменувань і може мати кілька значень (більше двох), а друга ознака виміряно за такою ж шкалою або за шкалою порядку, або за шкалою інтервального, або по шкалою пропорційною.
Цей коефіцієнт також розраховується за допомогою критерію хі-квадрат Пірсона, розрахункове значення якого підставляється в формулу:
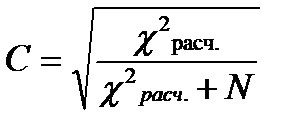
Таблиць з критичними значеннями для коефіцієнта взаємної спряженості Пірсона не існує. Тому надходять у такий спосіб:
1. Обчислюють розрахункове значення критерію хі-квадрат Пірсона.
2. Порівнюють його з критичним значенням для відповідного числа ступенів свободи.
3. Якщо # 967; 2 розр <χ 2 табл. то расхождения между рас-пределениями статистически недостоверны, или признаки изменяются несогласованно, или связи между признаками нет. Делается вывод об отсутствии взаимосвязи. Величину коэффициента С можно в этом случае не вычислять.
4. Якщо # 967; 2 розр ≥ # 967; 2 табл. то рас-ходіння між розподілами статистично достовірні, або ознаки змінюються узгоджено, або зв'язок між ознаками статистично значуща.
5. Далі обчислюється значення коефіцієнта взаємної спряженості Пірсона, яке і є мірою зв'язку. Чим більше це значення (величина цього коефіцієнта може бути тільки позитивною і змінюється від 0,00 до +1,00), тим сильніше взаємозв'язок.
Зверніть увагу на те, що обмеження у використанні цього коефіцієнта відповідають обмеженням критерію хі-квадрат Пірсона, а саме: обсяг вибірки повинен бути N≥30 і теоретична частота в осередках повинна бути f≥ 5.
Порівняння двох останніх коефіцієнтів показало, що в одних і тих же випадках коефіцієнт взаємної спряженості Пірсона дає кілька бóльшие значення міри зв'язку.
Слід враховувати при виборі міри зв'язку і те, що коефіцієнт взаємної спряженості Чупрова рекомендується використовувати в тих випадках, коли число градацій значень ознак невелика, так як цей коефіцієнт менше чевствітелен до кількості подій.