Л юбую систему управління. працюючу з цифровими сигналами, можна представити у вигляді рис. 2.44 (а), де стану вихідних сигналів Z, Y, X, W і т. Д. Визначаються значеннями входів А, В, С, D і т. Д. Роботу системи управління можна організувати, використовуючи комбінацію двох основних методів.
Найпростішим з цих методів є комбінаторна логіка. коли систему можна розбити на більш дрібні блоки, як на рис. 2.44 (б), з одним виходом у кожного блоку, причому стан виходу визначається тільки значеннями відповідних входів. Наприклад, навантажувальний вентиль гідравлічного насоса буде задіяний, якщо:
Насос включений AND
(Обрано режим «підвищити» AND не спрацював верхній кінцевий вимикач) OR
(Обрано режим «знизити» AND не спрацював нижній кінцевий вимикач)
Роботу цього навантажувального вентиля можна організувати за допомогою простої програми у вигляді багатоступінчастої схеми або логічної структури, як на рис. 2.45, але краще розробити стандартний спосіб створення програми на основі комбінаторної логіки.
Перший етап полягає в розбитті системи управління на ряд невеликих блоків, кожен з яких має один вихід і кілька входів. Далі для кожного виходу треба скласти так звану таблицю істинності, в якій повинні бути записані всі можливі стани входів і відповідні їм необхідні стану виходу. На рис. 2.46 (а) ми маємо вихід Z, що залежить від чотирьох входів А, В, С, D. Усього є 16 можливих комбінацій станів входів, a Z активізується (т. Е. Є істинним) тільки для чотирьох з них. Це відразу можна відобразити у вигляді багатоступінчастої схеми на рис. 2.46 (б) або логічної схеми на рис. 2.46 (в), де кожна ланка або вентиль AND відповідають одному рядку таблиці істинності.
Використання таблиць істинності для синтезу схем комбінаторної логіки безпосередньо призводить до структури, що складається з елементів AND / OR і технічною мовою званої «сумою творів».
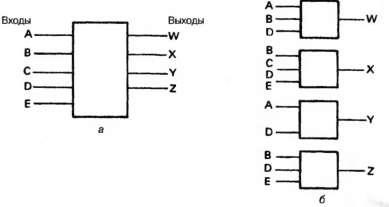
Мал. 2.44. Комбінаторна логіка: (а) подання на високому рівні; (Б) розбивка на менші блоки
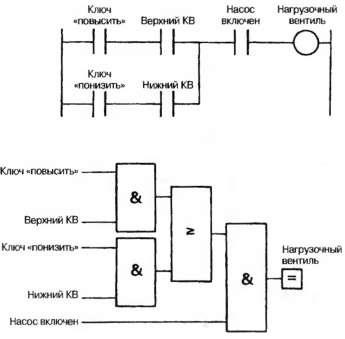
Мал. 2.45. Комбінаторна логіка в багатоступінчастої схемою і в логічних позначеннях
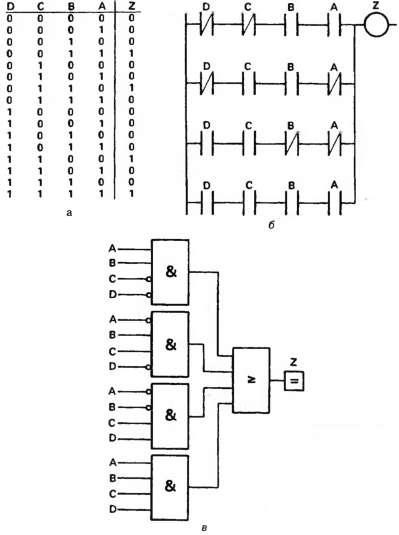
Мал. 2.46. Комбінаторна логіка як наслідок таблиці істинності: (а) таблиця істинності; (Б) сходова реалізація таблиці істинності; (В) реалізація у вигляді логічної схеми
Виникає природне запитання: «Чи є така структура найпростішої?» Відповідь буде негативним, так як існують такі методи, як карти Карно і булева алгебра, що дають більш просте рішення. Якщо структура створюється з логічних вентилів або реле, то бажано обійтися мінімальною кількістю вентилів або контактів, щоб знизити витрати на проектування. При написанні програми для ПЛК додаткових контактів не потрібно, тому головною метою має бути прозорість роботи програми, а не її простота. Одне з спрощень, яке завжди рекомендується робити (знову ж для прозорості), полягає у винесенні з ланок загального контакту, як показано на рис. 2.47.
Як приклад розглянемо пульт управління приводом насосів, зображений на рис. 2.48 (а). Заради дешевизни трехпозіці-ційний перемикач з'єднаний безпосередньо з двома групами контактів, як показано на рис. 2.48 (б) (на практиці так робити не
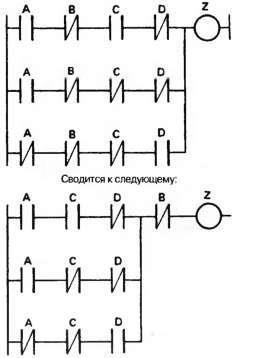
Мал. 2.47. Спрощення комбінаторної логіки
рекомендується, так як при відмові джерела живлення обидва насоса будуть включеними). Таблиця істинності для цього випадку призводить до багатоступеневої схемою на рис. 2.48 (в), але схема мінімальної складності має вигляд рис. 2.48 (г). Остання, однак, не відображає роботу перемикача і тому дещо ускладнює виявлення несправностей.
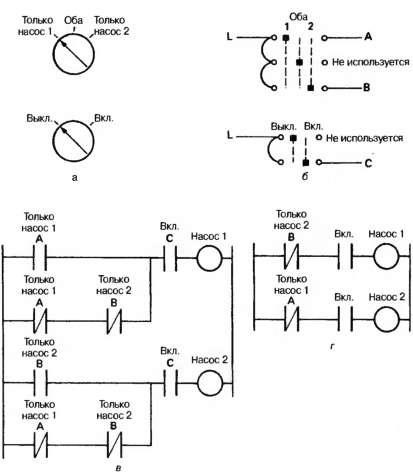
Мал. 2.48. Мінімізація не сприяє прозорості: (а) пульт управління; (Б) підключення пульта; (В) програма на основі таблиці істинності; (Г) програма мінімальної складності