




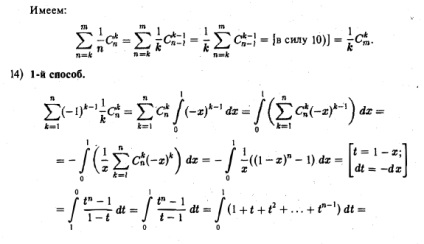

цьому параграфі буде доведений ряд співвідношень для біноміальних коефіцієнтів. Всі вони цікаві самі по собі і багато будуть використовуватися нами в подальшому. Однак не менш цікаві способи їх докази (або отримання). Ми будемо, як правило, пропонувати докази, які виходять із комбінаторної природи співвідношень. Загальна схема міркувань тут така. Нехай доводиться тотожність По виду лівої і правої частин реконструюється завдання на підрахунок чистий комбінацій певного виду (п, т. Виступають в ролі параметрів), вирішуючи яку одним способом, отримуємо в якості відповіді. а іншим способом - У ніжепріводімих співвідношеннях значення параметрів передбачаються такими, щоб усі біноміальні коефіцієнти мали сенс (наприклад, якщо у формулі присутній CJ, то передбачається, що Комбінаторні тотожності Мають місце наступні тотожності: 1) Кожному до -елементному подмножеству n-елементного безлічі поставимо у відповідність його доповнення до всього безлічі. Неважко бачити, що при цьому задається взаємно однозначна відповідність між до -елементнимі і (п - Л;) - елементними подмножествами n-елементного безлічі. Якщо між двома кінцевими множинами існує взаємно однозначна відповідність, то ці множини містять однакову кількість елементів. Таким чином, число поєднань з п по к збігається з числом сполучень, з п по п - к. 2) Нехай в парламенті п депутатів, включно зі спікером. Підрахуємо число способів скласти парламентську делегацію з до людей. З одного боку, це число поєднань СJ. Зробимо підрахунок по-іншому. Для того щоб сформувати делегацію, що включає спікера, потрібно з п - I рядових депутатів вибрати до - 1; це можна зробити способами. Якщо ж спікер в делегацію не входить, то її членів можна вибрати. способами (з п - 1 рядових депутатів обирається *; людина). Таким чином, всього є. способів скласти делегацію. 3) 2П - число всіх підмножин n-елементного безлічі. Так як CJ - число всіх його fc-елементних підмножин, то підсумувавши Cj по к від 0 до п, знову отримаємо загальне число всіх підмножин. Інший спосіб докази полягає в застосуванні формули бінома Ньютона Поклавши в ній х = 1, отримаємо необхідну. 4) Тотожність доводиться підстановкою в наведеній вище формулі х = -1. Наведемо також комбинаторное доказатиьство. Знайдемо кількість підмножин n-елементного безлічі, що мають парне число елементів. Воно збігається з кількістю способів скласти парламентську делегацію з парного числа осіб, якщо в парламенті всього п депутатів. Довільна делегація такого виду може бути отримана в результаті виконання наступної процедури. Спочатку щодо кожного з депутатів, не рахуючи спікера, будемо приймати рішення, увійде даний депутат в делегацію чи ні. Згідно з правилом твори, ці рішення могуг бути винесені 2П
'Способами. Спікер включається до складу делегації тільки в тому випадку, коли в ній непарне число «рядових» депутатів. Таким чином, загальне число делегацій з парним числом членів одно 2п
1, Оскільки обшее число підмножин є 2П, підмножин з непарним числом елементів також 2П_ |, тобто стільки ж, скільки і з парним числом елементів. Значить, оскільки частини записаного рівності виражають собою число підмножин n-елементного безлічі відповідно з непарним і парним числом елементів. Отримане рівність рівносильно доказуваному. 5) Дане співвідношення є іншою формою запису попереднього тотожності. Комбінаторні тотожності 6) Вирішимо таке завдання. Є т чоловіків і п жінок. З них потрібно сформувати делегацію з до людей. Яким числом способів це можна зробити? Отвег очевидний: з £ + п. Будемо класифікувати делегації по числу чоловіків. Якщо в делегацію входять з чоловіків і k - а жінок, то чоловіків можна вибрати способами, а женшін - способами; значить, число делегацій з з> чоловіками одно. Підсумовуючи
a по s від 0 до до, отримаємо обшее число делегацій. 7) Для доказу досить в попередньому співвідношенні покласти застосувати 1). 8) Доказ тотожності може бути отримано з вирішення наступного завдання: Яким числом способів можна з п кандидатів вибрати до депутатів і серед останніх спікера? Депутати обираються З £ способами, після чого спікер обирається до способами; таким чином, загальне число способів дорівнює С "к. Те ж число можна підрахувати по-іншому. Будемо спочатку (всенародним голосуванням) обирати спікера (з п кандидатів), а потім з решти п - 1 кандидата - ще депутата. Зазначена процедура може бути виконана п • J способами. Доведено, що. Звідси випливає корисне рекурентне співвідношення. застосовуючи яке кілька (точніше: к) раз, можна знову вивести формулу для числа сполучень 9) Це тотожність - узагальнення попереднього (якщо в 9) покласти m = 1, то отримаємо 8)) і може бути доведено за допомогою рішення задачі, Таюса є узагальненням раніше рассмотредаой: Яким числом способів можна вибрати з п кандидатів до депутатів і серед останніх т членів президії? 10) 1-й спосіб. Доведемо тотожність математичної індукції по к. База індукції. При до = 0 маємо вірне рівність: Індукційний крок. Нехай доказувана твердження вірне при. Додавши до обох частин рівності. отримаємо Таким чином, співвідношення 10) справедливо і при. 2-й спосіб. Загальна кількість (-елементних підмножин безлічі одно. (Правій частині доказуваного тотожності). Будемо класифікувати зазначені підмножини по їх найбільшому елементу, який, очевидно, приймає значення. Знайдемо число підмножин з найбільшим елементом т + р 4-1. Оскільки найбільший елемент вже обраний , що залишилися m елементів вибираються з безлічі значить, число таких підмножин одно Підсумовуючи. знову отримаємо загальне число -елементних підмножин (ліву частину доказуваного тотожності). 11) Тотожність доводиться на основі попереднього: 12) Виріши м задачу: Яким числом способів можна з п кандидатів вибрати т депутатів і серед депутатів деяких (можливо, всіх, а може бути, нікого) нагородити. З одного боку, депутати вибираються способами, а нагороджені виділяються 2т способами (стільки підмножин має безліч з m елементів), і, отже, відповідь до задачі. З іншого боку, якщо число нагороджених депутатів одно к. То їх можна вибрати способами, після чого інші m - до депутатів обираються способами. Підсумовуючи по к від 0 до тп, знову Комбінаторні тотожності отримаємо відповідь до розглянутій задачі. Тотожність доведено. 13) Використовуючи співвідношення 8), перетворимо загальний член суми: 2-й спосіб. Скориставшись 13) тотожністю, заметм і в отриманій подвійний сумі поміняємо порядок підсумовування