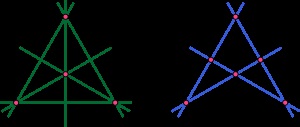
У проективної геометрії конфігурація на площині складається з кінцевого безлічі точок і кінцевої конфігурації прямих. таких, що кожна точка инцидентна деякого числа прямих і кожна пряма инцидентна деякого числа точок [2].
Хоча деякі специфічні конфігурації вивчалися раніше (наприклад, Томасом Кіркманом [en] в 1849), формальне вивчення конфігурацій почав вперше Теодор Рейє [en] в 1876 у другому виданні його книги Geometrie der Lage (Геометрія позицій), в контексті обговорення теореми Дезарга. Ернст Стейніц написав свою дисертацію на цю тему в 1894 і конфігурації були полулярізіровани в 1932 Гильбертом і Кон-Воссеном в книзі Anschauliche Geometrie (Наочна геометрія), яка потім була переведена на англійську [3].
Конфігурації можна вивчати або як конкретне безліч точок і прямих в конкретної геометрії, наприклад, на евклідової або проективної площині (в цьому випадку говорять про реалізацію в цій геометрії), або як абстрактну геометрію инцидентности. В останньому випадку конфігурації тісно пов'язані з регулярними гіперграфах і бірегулярнимі [en] дводольними графами. але з додатковим обмеженням - будь-які дві точки структури инцидентности можуть бути асоційовані максимум з одній прямій, а будь-які дві прямі можуть бути асоційовані максимум з однією точкою. Тобто обхват відповідного двудольного графа (граф Леві конфігурації) повинен бути щонайменше дорівнює шести.
Конфігурація на площині позначається як (pγℓπ), де p - число точок, ℓ - число прямих, γ - число прямих, що проходять через кожну точку, а π - число точок на кожній прямій. Для цих чисел повинно виконуватися співвідношення
оскільки цей твір дорівнює числу інціденцій точка-пряма (прапорів).
Конфігурації з тим же символом не зобов'язані бути ізоморфними як структур инцидентности. Наприклад, існує три різних конфігурації (93 93) - конфігурація Паппа і дві менш помітні зміни.
У деяких конфігураціях p = ℓ а тому, γ = π. Вони називаються симетричними або збалансованими [4] конфігураціями і зазвичай в позначеннях повторення опускається. Наприклад, (93 93) скорочується до (93).
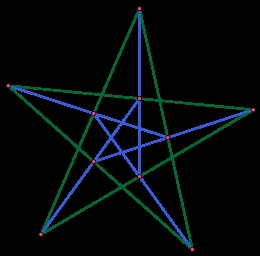
Конфігурація (103), що не ізоморфна по инцидентности конфігурації Дезарга
Найбільш помітні наступні проектні конфігурації:
- (11), найпростіша можлива конфігурація, що складається з точки на прямій. З огляду на тривіальності часто не розглядається.
- (32), трикутник. Кожна з трьох сторін містить дві з трьох вершин, і навпаки. Узагальнено, будь багатокутник з n сторонами утворює конфігурацію типу (n2)
- (43 62) і (62 43), повний чотирикутник і повний четирехсторонніке [1] відповідно.
- (73), Площина Фано. Ця конфігурація існує як абстрактна геометрія инцидентности. але вона не може бути побудована на евклідової площини.
- (83), конфігурація Мебіуса - Кантора. Ця конфігурація складається з двох чотирикутників, одночасно описаних і вписаних відносно один одного. Конфігурацію можна побудувати на евклідової площини, але рівняння, її визначають, мають нетривіальні рішення в комплексних числах.
- (93), конфігурація Паппа.
- (94 123), Конфігурація Гессе дев'яти точок перегину кубики на комплексної проективної площині і дванадцяти прямих, кожна з яких містить по три точки. Ця конфігурація має ту ж властивість, що і площину Фано, а саме, що вона містить всі прямі, що проходять через будь-які дві точки конфігурації. Конфігурації з такими властивостями відомі як конфігурації Сильвестер-Галлай. Для цих змін по теоремі Сильвестра не можуть існувати координати в дійсних числах [5].
- (103), конфігурація Дезарга.
- (125 302), подвійна шістка Шлефлі. утворена 12 з 27 прямих кубічної поверхні [en]
- (153), конфігурація Кремони - Річмонда. утворена 15 прямими, що не входять в подвійну шістку, і 15 дотичними площинами
- (124 163), Конфігурація Рейє.
- (166), конфігурація Куммера [en].
- (273), конфігурація Грея
- (6015), конфігурація Клейна [en].
Проективно двоїстої конфігурацією для (pγlπ) є конфігурація (lπpγ), в якій ролі «точок» і «прямих» міняються місцями. Тому конфігурації йдуть подвійними парами, за винятком випадків, коли двоїста конфігурація ізоморфна вихідної. Ці виключення називаються самодвоїстих конфігураціями і в цих випадках p = l [6].
Число неізоморфних конфігурацій типу (n3), починаючи з n = 7, складають послідовність
Ці числа підраховані як абстрактні структури инцидентности незалежно від можливості їх реалізації [7]. Як пише Гроппа [8]. дев'ять з десяти конфігурацій (103) і всі конфігурації (113) і (123) дозволяють реалізацію в евклідовому просторі, але для всіх n ≥ 16 є щонайменше одна нереалізована конфігурація (n3). Гроппа також вказує давню помилку в цій послідовності - в статті 1895 року було спроба перерахувати всі конфігурації (123) і 228 з них були знайдені, але 229-я конфігурація не була відкрита аж до 1988.
Побудова симетричних конфігурацій
Є кілька методів побудови конфігурацій, зазвичай початківців з уже відомих конфігурацій. Деякі найпростіші з цих методів будують симетричні (pγ) конфігурації.
Будь-яка кінцева проективна площину порядку n є конфігурацією ((n 2 + n + 1) n + 1). Нехай Π - проективна площину порядку n. Видалимо з Π точку P і всі прямі Π, що проходять через P (але не точки, що лежать на цих прямих, за винятком точки P) і видалимо пряму l. що не проходить через P. і всі крапки, що лежать на цій прямій. В результаті отримаємо конфігурацію типу ((n 2 - 1) n). Якщо при побудові виберемо пряму l. що проходить через P. отримаємо конфігурацію типу ((n 2) n). Оскільки відомо, що проектні площині існують для всіх порядків n. є ступенями простих чисел, ці побудови забезпечують нескінченне сімейство симетричних конфігурацій.
Не всі конфігурації реалізовані, наприклад, конфігурація (437) не існує [9]. Однак Груп [10] дав побудова, яке показує, що для k ≥ 3 конфігурація (pk) існує для всіх p ≥ 2 lk + 1, де lk є довжиною оптимальної лінійки Голомба порядку k.
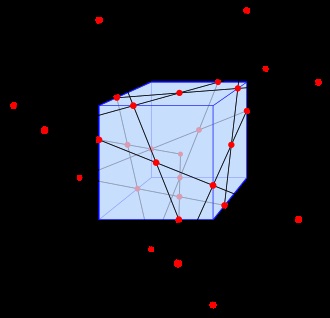
Концепція конфігурації може бути узагальнена на більш високі розмірності, наприклад для точок і прямих чи площин в просторі. У цьому випадку обмеження, що ніякі дві точки не можуть лежати на більш ніж двох прямих, можна послабити, оскільки дві точки можуть належати більш ніж одній площині.
У тривимірному просторі цікавими є
- Конфігурація Мебіуса. що складається з двох взаємно вписаних тетраедрів
- Конфігурація Рейє. що складається з дванадцяти точок і дванадцяти площин з шістьма точками на кожній площині і шістьма площинами, що проходять через кожну точку
- Конфігурація Грея. що складається з 27 точок решітки 3 × 3 × 3 і 27 ортогональних прямих, що проходять через них
- Подвійна шістка Шлефлі. що складається з 30 точок і 12 прямих, по дві прямі на точку і по п'ять точок на одній прямій.
Подальше узагальнення виходить в тривимірному просторі при розгляді инцидентности точок, прямих і площин, тобто j -простору при 0 ≤ j <3, где каждое j -пространство инцидентно Njkk -пространствам (j ≠ k ). Если обозначить через Njj число j -пространств, такую конфигурацию можно представить в виде матрицы :
Підхід можна узагальнювати для інших розмірностей n. де 0 ≤ j
Схожі статті