Дислокаціями називають лінійні недосконалості або одномірні дефекти кристалічних решіток реальних металів, що представляють собою особливі порушення кристалічної будови, пов'язані з відхиленнями реальних кристалів від ідеального їх будови.
Дислокації бувають крайові, гвинтові і змішані криволінійні. Виникають вони в металах в процесі кристалізації, пластичній деформації і з інших причин, що викликають створення полів напружень в кристалічній решітці, що призводять до відповідних локальних деформацій і зсувів.
Теорія дислокацій дозволила пояснити, чому реальна міцність металів разюче відрізняється від теоретичної міцності (підрахованої з урахуванням сил міжатомної взаємодії).
Уявімо собі, що в кристалічній решітці з яких-небудь причин з'явилася зайва напівплощина атомів, так звана екстраплоскості Q (рис. 1.4). Край 3-3 'такій площині утворює лінійний дефект (недосконалість) решітки, який називають крайової дислокацією. Якщо така дислокація знаходиться вгорі, то її вважають позитивною і позначають знаком ┬; крайову дислокацію, що знаходиться внизу (негативну), позначають знаком ┴.
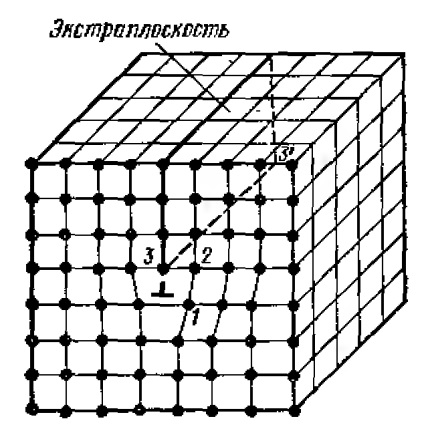
Малюнок 1.4. Дислокація в кристалічній решітці.
Крайова дислокація може сягати в довжину на багато тисяч періодів решітки, її лінія не може бути прямий і, володіючи поверхневий натяг, вона прагне замкнутися в контур. Навколо дислокації виникає зона пружного спотворення решітки. Ширина дислокацій, т. Е. Відстань від центру дефекту до місця решітки без спотворення, невелика і дорівнює кільком міжатомним відстаням.
Внаслідок спотворення решітки в районі дислокації остання легко може зміщуватися вправо або вліво від нейтрального положення і встановлювати зв'язок крайових своїх атомів 3 з атомами 1 (див. Рис. 1.4), а сусідня справа (зліва) напівплощина буде при цьому переходити в проміжне положення, перетворюючись тим самим в екстраплоскості і утворюючи дислокацію уздовж крайових атомів 2 і т. д. Таким чином, дислокація може переміщатися (вірніше - передаватися як естафета) уздовж деякої площини ковзання, розташованої перпендикулярно до екстраплоскості сті Q.
Дислокації в металах можна спостерігати за допомогою електронного мікроскопа.
Теоретично, при елементарному пластичному зсуві (рис. 1.5), якщо врахувати сили міжатомної взаємодії для кожної пари сполучених атомів (щодо площині ковзання АА) 1-1 ', 2-2' і т. Д. І враховуючи, що в площині ковзання реального металевого кристала є близько 1014 атомів на кожен см 2 перерізу, потрібно надзвичайно велике зусилля (для технічного заліза, як уже зазначалося, в десятки разів більше, ніж це реально спостерігається).
Згідно дислокационной теорії пластичний зсув в металі слід розглядати як процес естафетного переміщення дислокацій. Спрощена схема цього процесу представлена на рис. 1.6.
В результаті наявності дислокації (рис. 23а) в кристалі по обидва боки ковзання АА виникає спотворене стан кристалічної решітки з порушенням порядку ідеальних зв'язків між атомами. У цьому випадку досить буде прикласти невелике зовнішнє зусилля Р (значно менше сили Р для ідеальної решітки-рис. 1.6б), щоб викликати распростране-
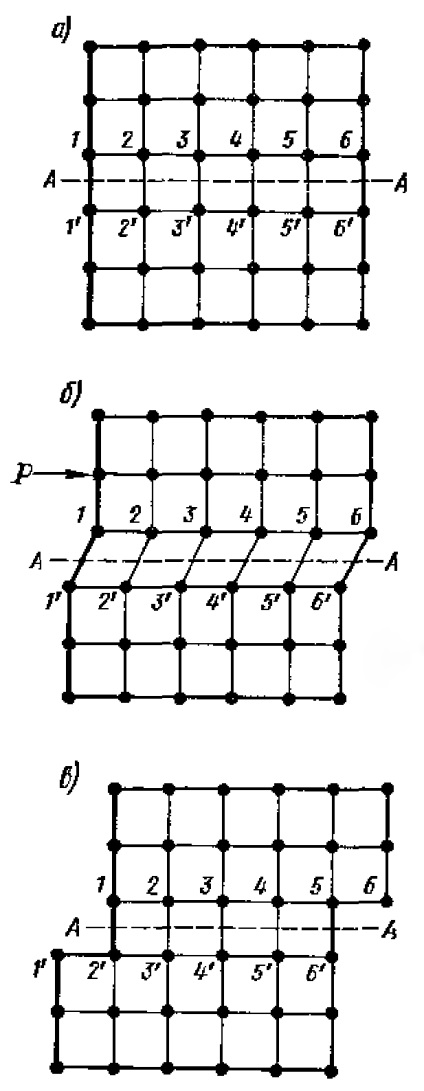
Малюнок 1.5. Пластичний зрушення в ідеальній кристалічній решітці:
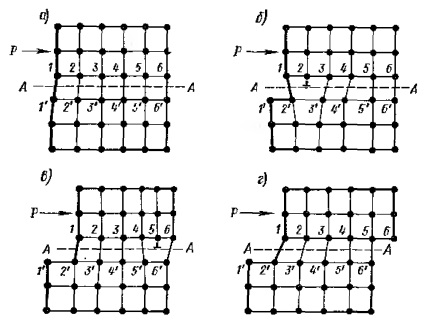
Малюнок 1.6. Дислокаційна схема пластичного зсуву.
ня хвилі послідовних приватних зсувів вертикальних рядів атомів над площиною ковзання АА, що не перевищують за величиною одного межатомного відстані. В результаті проходження цієї хвилі дислокація, як своєрідна естафета, буде послідовно передаватися рядах атомів 3, 4. і в певний момент займе положення, представлене на рис. 1.6В. У підсумку ж передачі руху від приватного зміщення ряду атомів 1 дислокація вийде на поверхню і зникне, як це показано на рис. 1.6г. Отже, кінцевим результатом переміщення дислокації уздовж площини ковзання АА з'явився зрушення на одне міжатомна відстань, причому для здійснення цього зсуву знадобилося значно менше зусилля, ніж при відсутності дислокації.
Звідси можна зробити висновок, що процес зсуву в кристалі відбувається тим легше, чим більше дислокацій є в металі. Навпаки, чим менше в металі таких дислокацій, тим менше можливостей для зсуву і тим міцніше метал. У металі, в якому не утворюються дислокації, зрушення можливий тільки за рахунок одночасного зсуву (як цілого) однієї частини кристала щодо іншої.
У цьому випадку міцність бездислокаційних металу повинна бути рівна теоретичної (точка 1 на рис. 1.7). Міцність ниткоподібних металевих кристалів - так званих вусів (точка 2 на рис. 1.7) - виявилася ближче до теоретичної, що, згідно з, припущеннями, обумовлено досить малою кількістю дислокацій. Так, наприклад, для ниткоподібних кристалів заліза межа міцності на розрив становить 140 МН / м2 (МПа).
Велике підвищення міцності металу зі збільшенням досконалості його кристалічної будови (на прикладі ниткоподібних кристалів) є переконливим підтвердженням теорії дислокації.
Крім отримання бездислокаційних металевих кристалів існує інший шлях зміцнення металів. Виявляється, що реальна міцність металів падає зі збільшенням числа дислокацій тільки спочатку. Досягнувши мінімального значення при деякої критичної щільності дислокацій (рис. 1.7), реальна міцність знову починає зростати. Підвищення реальної міцності із зростанням щільності дислокацій пояснюється тим, що при цьому виникають не тільки паралельні один одному дислокації, а й дислокації в різних площинах і напрямах. Такі дислокації будуть заважати один одному переміщатися, т. Е. В елементарний акт пластичної деформації залучатиметься одночасно все більше число атомів, і реальна міцність металу підвищиться.
Традиційними способами зміцнення металів, які ведуть до збільшення щільності дислокацій, є механічний наклеп, подрібнення зерна і загальне фрагментованість кристалів в результаті термообробки. Деякі давно відомі методи легування (наприклад, внесення в решітку основного металу чужорідних атомів), що створюють всякого роду недосконалості та викривлення кристалічної решітки, перешкоджають вільному переміщенню дислокацій або блокують їх. Сюди ж відносяться способи освіти структур з так званими зміцнюючих фазами (наприклад, дисперсійне твердіння).
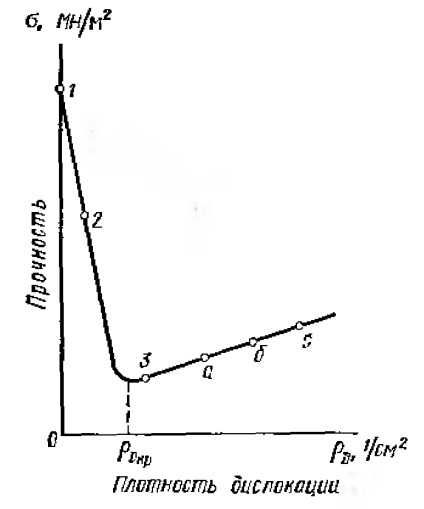
Однак у всіх цих випадках зміцнення далеко не досягає теоретичного значення. Отже, в тій чи іншій мірі наявність дислокацій в реальному металевому кристалі є причиною зниження його міцності за рахунок прояву здатності пластично деформуватися при напружених, менших теоретичного рівня.
Слід зазначити, що взаємодії дислокацій один з одним і з іншими дефектами металу настільки складні, що на основі простих дислокаційних теорій не можна передбачати міцність твердих тіл. Однак, теорія дислокацій дозволяє якісно характеризувати процеси деформації, руйнування та зміцнення твердих тіл.
Теорія дислокацій на сьогоднішній день стала невід'ємною частиною фізики твердого тіла і фізичного металознавства. Всі процеси, що протікають в металах і сплавах, а також формування їх властивостей нерозривно пов'язані з характером і щільністю дефектів кристалічної будови і, в першу чергу, дислокацій. Так, пластична деформація, зазвичай представляє собою внутрізеренний зрушення, здійснюється, як про це було сказало вище, шляхом руху дислокацій.
Теорія дислокацій пояснює залежність між деформаціями і напруженнями, розкриває причини деформаційного зміцнення (наклепу). Чим більше щільність дислокацій при рівномірному їх розподілі, тим вище міцність металу.
Зміцнення твердих розчинів не можна пояснити без урахування взаємодії розчинених атомів з дефектами кристалічної будови і, в першу чергу, з дислокаціями.
Навколо дислокацій можуть створюватися скупчення чужорідних атомів, які отримали назву «атмосфер Котредла». Утворення таких скупчень (особливо впровадженими атомами) може в значній мірі ускладнювати рух дислокацій збільшуючи тим самим опір пластичної деформації.
Процес руйнування металів неможливо пояснити, що не грунтуючись на теорії дислокацій, оскільки руйнування і пластична деформація нерозривно пов'язані між собою. Запропоновано різні дислокаційні моделі освіти зародків тріщин, що виникають завдяки скупченню дислокацій перед бар'єрами.
Чи не залучаючи теорію дислокацій, не можна пояснити повзучість металів, оскільки вона визначається процесами ковзання і «переповзання» дислокацій.
Дислокації істотно впливають на процес дифузії. Так як дислокації можуть бути джерелом вакансій (атомних дірок в кристалічній решітці), то вони сприяють прискоренню дифузійних процесів. Дислокації можуть зменшувати роботу утворення зародків нової фази, будучи областями переважного її виділення (наприклад, при дисперсионном твердінні).
Теорія дислокацій визначає характер взаємодії дислокації з дисперсними частками інших фаз і розкриває причини зміцнення старіючих сплавів.
Отже, багато питань металознавства нерозривно пов'язані з теорією дислокацій. Теорія дислокацій підказала шляхи реалізації прихованих резервів міцності металів, які полягають в повнішому використанні сил міжатомних зв'язків в кристалічній решітці. Це виразилося, зокрема, в розробці принципово нових, практично бездислокаційних матеріалів - ниткоподібних кристалів металів і інших кристалічних речовин (графіту, окислів і ін.), Що володіють надзвичайно високою міцністю в підвищенні міцності раніше відомих марок стали шляхом комбінованої термомеханічної обробки (ТМО).
Дислокаційна теорія слугує подальшому розвитку металознавства і його практичного застосування.
Контрольне завдання №2
Визначити несучу здатність N. кН, прямого розтягнутого стикового шва двох листів перетином 500х25мм, зі сталі С275. Контроль якості шва - візуальний.
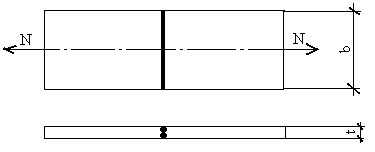
Рішення. Визначаємо розрахунковий опір сталі і зварного з'єднання, використовуючи дані таблиці 51, / 3 /. Для листової сталі С275 товщиною 25мм розрахунковий опір за межею текучості
Ry = 270 МПа (27 кН / см 2); для зварного стикового з'єднання, що працює на розтяг і при відсутності фізичного контролю якості шва розрахунковий опір по таблиці 3, / 3 /, Rwy = 0,85Ry = 0,85 ∙ 270 =
= 229,5 МПа = 22,95 кН / см 2.
Несучу здатність стикового шва N. кН, визначаємо з умови забезпечення міцності зварних стикових з'єднань, що визначаються за формулою (146), / 3 /