Мета роботи: визначення коефіцієнта самоіндукції котушки методом вимірювання її повного електричного опору (імпедансу) по змін-ному і постійного струму.
Прилади й устаткування: котушка індуктивності (L), змінний опір (Rпер.), Джерело постійного струму (# 949;), міліамперметр змінного і постійного струму (мА), вольтметр змінного струму (
V), вольтметр постійного струму (= V), генератор електричних коливань (ЗГ), джерело постійного струму (# 949;).
У просторі, що оточує електричні струми і постійні магніти, виникає силове поле, що називається магнітним. Наявність його виявляється по силовому дії на внесення провідники або постійні магніти.
Ампер встановив, що сила. з якої магнітне поле діє на елемент провідника зі струмом прямо пропорційна силі струму I і вектор-ному твору елемента на магнітну Індуктори цію:
Модуль сили Ампера визначається за формулою
де - кут між векторами і; і.
Таким чином, вектор магнітної індукції є силовий характе--них магнітного поля. Останнє зображують за допомогою ліній магнітної індукції - ліній, дотичні до яких в кожній точці збігаються з напрямом вектора. Магнітна стрілка встановлюється уздовж дотичної до лінії магнітної ін-продукції, причому її північний кінець N указує напрямок вектора.
Закон Ампера дозволяє визначити одиницю виміру магнітної індукції. Нехай елемент провідника Cток силою I перпендикулярний лініям магнітної індукції однорідного поля. Тоді модуль сили Ампера дорівнює
при = π / 2 і sin = 1.
Одиниця виміру магнітної індукції - Тесла (Тл).
1 Тесла - магнітна індукція од-нородного поля, що діє з силою в 1Н на кожен метр довжини прямол-лінійного провідника, розташованого перпендикулярно лініям магнітної індукції, якщо з цього про-воднику йде струм силою 1А:
Потоком вектора магнітної індукції (магнітним потоком) через пло-ках dS називається скалярна фізична величина, що дорівнює
де Вn = Вcos - проекція вектора на напрямок одиничного вектора нормалі до площадки dS; - кут між векторами і; - вектор, модуль якого дорівнює dS (), а напрямок збігається з напрямком нормалі до площадки dS (рис. 1).
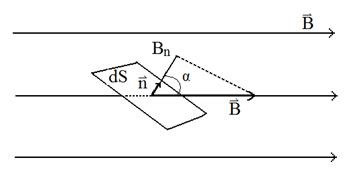
Для однорідного поля і плоскої поверхні, перпендикулярній вектору,
Вn = В = const і Ф = ВS.
З останньої формули визначається одиниця виміру магнітно-го потоку - Вебер (Вб).
1 Вебер - магнітний потік, що проходить через плоску по-поверхню площею 1м 2. перпендикулярну лініям магнітної індукції однорідного поля, індукція якого дорівнює 1 Теслі:
Теорема Гаусса для магнітного поля: потік вектора магнітної індукції через будь-яку замкнену поверхню дорівнює нулю, тобто
Ця теорема відображає відсутність магнітних зарядів, внаслідок чого ли-нии магнітної індукції не мають ні початку, ні кінця і є замкну-тими.
Електричний струм, що йде по замкнутому контуру, в навколишньому просторі створює маг-нітних поле, індукція якого, згідно із законом Біо-Савара-Лапласа, прямо про-пропорційна силі струму. Тому магнітний потік Ф пропорційний силі струму I в контурі:
де L - коефіцієнт самоіндукції, або індуктивність контуру. З цього ви-ражения визначається одиниця виміру індуктивності - Генрі (Гн).
1 Генрі - індуктив-ність такого контуру, магнітний потік самоіндукції якого при силі струму в 1А дорівнює 1 Вебером:
Фарадей відкрив закон: при зміні магнітного потоку, що пронизує поверхню, натягнуту на замкнутий проводить контур, в останньому метушні-кає електрорушійна сила (ЕРС) індукції:
Знак «мінус» у цій формулі є математичним виразом пра-вила Ленца: індукційний струм в контурі має завжди такий напрямок, при якому створюється їм магнітне поле перешкоджає зміні магнітного потоку.
Таким чином, при зміні сили струму в контурі змінюється і зчеплений-ний з ним магнітний потік і, отже, індукує ЕРС.
Виникнення ЕРС в провідному контурі при зміні в ньому сили струму на-ни опиняються самоіндукцією.
Застосовуючи до самоіндукції закон Фарадея, отримаємо, що ЕРС самоіндукції
Якщо контур не деформується, то L = const і
Значить, на кінцях котушки виникає ЕРС самоіндукції, що перешкоджає через трансформаційних змін сили струму.
Визначення коефіцієнта самоіндукції
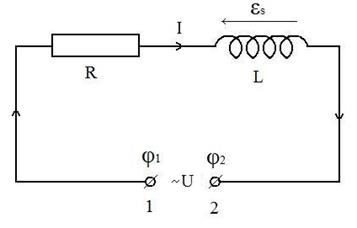
Розглянемо електричний ланцюг, що складається з котушки індуктивності L. Котушка має активну (омічний) опір R і індуктивне (реактивне) опір # 969; L, де # 969; - циклічна частота змінного струму; L - індуктивність котушки. Бу-дем вважати, що омічний опір котушки зосереджено в опору-лення R, включеному послідовно з нею (рис. 2). На контакти 1 і 2 подає-ся змінну напругу
U з циклічною частотою # 969 ;.
Нехай в даний момент часу потенціал першого контакту # 966; 1 більше потенціалу другого контакту # 966; 2. Тоді струм I йде зліва направо.
Припустимо, що сила струму I збільшується, тобто
Тоді, відповідно до закону Фарадея, на кінцях котушки L виникає ЕРС са-моіндукціі, напрямок якої протилежно напрямку струму I в ланцюзі:
Якщо вхідна напруга
U змінюється по гармонійному закону, то
де Um - амплітуда напруги.
Запишемо закон Ома для цього неоднорідної ділянки кола:
Приватне рішення диференціального рівняння (2) має вигляд
де Im - амплітуда сили струму, - початкова фаза коливань струму.
Знайдемо першу похідну:
Вирази (7.3) і (7.4) підставимо в формулу (7.2):
Рівність (7.8) буде справедливо для будь-якого моменту часу t при усло-вії # 947; - # 946; = 0 і # 947; = # 946 ;. Тоді з (8) отримуємо
З рівності (9) випливає, що
є повним електричним опором (імпедансом) ділянки кола, що включає активний опір R і індуктивне опір # 969; L котушки індуктивності.
На практиці за допомогою вольтметра і амперметра вимірюються ефективні (дію-щие) значення змінних напруг і сили струму, пов'язаний-ні з амплітудами наступним чином:
З виразу (10) отримуємо
(# 969; L) 2 = Z 2 - R 2
Отже, вимірюючи повний електричний опір Z котушки індуктивності при змінному струмі і її івано-франківців-ське опір R при постійному струмі, можна знайти індуктивність котушки L.
Порядок виконання роботи
1. Зібрати робочу схему для визначення повного електричного опору Z (імпедансу) котушки індуктивності при змінному то-ке (рис. 3).
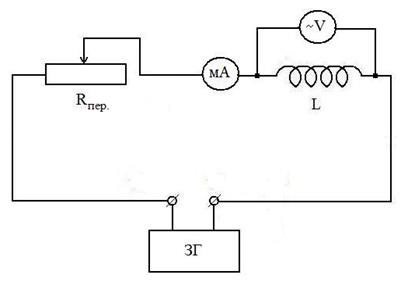
2. Встановити максимальне значення змінного опору Rпер. .
3. Включити генератор ЗГ.
4. Змінюючи опір Rпер .. отримати п'ять значень сили струму Iефф і виміряти відповідні напруги Uефф на котушці індуктивності.
5. Результати вимірювань занести в таблицю 1.
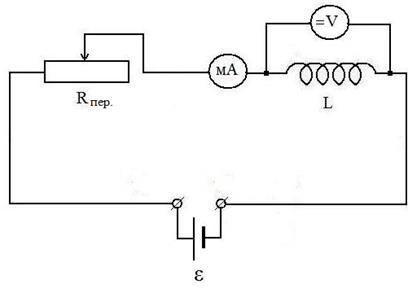
11. Обчислити омические опору R котушки індуктивності і знайти їх середнє значення Rср. .
при частоті # 957; = 1000 Гц визначити коефіцієнт самоіндукції L котушки.
1. Що таке магнітне поле? Що таке лінії індукції магнітного поля?
2. Як формулюється закон Ампера? Одиниця виміру індукції магнітно-го поля.
3. Дати визначення потоку вектора магнітної індукції. Одиниця його вимірювання.
4. Що таке індуктивність контуру? Одиниця її виміру.
5. Сформулювати закон Фарадея і правило Ленца.
6. У чому полягає явище самоіндукції? Е Д С. самоіндукції котушки.
7.Явленіе взаємної індукції. Практичне застосування цього явища.
8.Напісать рівняння Максвелла в інтегральній формі.
9. Вивести робочі формули для розрахунку повного опору (імпедансу) і ко-коефіцієнта самоіндукції котушки індуктивності.