Парний критерій Т - Вілкоксона
Для вирішення завдань, в яких здійснюється порівняння двох рядів чисел психолог може використовувати парний критерій Т - Вілкоксона. Цей критерій застосовується для оцінки відмінностей експериментальних даних, отриманих в двох різних умовах на одній і тій же вибірці випробуваних. Він дозволяє виявити не тільки спрямованість змін, але і їх вираженість, т. Е. Він дозволяє встановити, наскільки зрушення показників в якомусь одному напрямку є більш інтенсивним, ніж в іншому.
Критерій Т заснований на ранжируванні абсолютних величин різниці між двома рядами вибіркових значень в першому і другому експерименті (наприклад, до і після будь-якого впливу). Ранжування абсолютних величин означає, що знаки різниць не враховуються, проте в подальшому поряд із загальною сумою рангів знаходиться окремо сума рангів, як для позитивних, так і для негативних зрушень. Якщо інтенсивність зсуву в одному напрямку виявляється більшою, то і відповідна сума рангів також виявляється більше. Цей зсув називається типовим, а протилежний, менший за сумою рангів зрушення - нетиповим. Ці два зсуву виявляються додатковими один одному. Критерій Т - Вілкоксона базується на величині нетипового зсуву, який називається
Приклад. Психолог проводить з молодшими школярами корекційну роботу по формуванню навичок уваги, використовуючи для оцінки результатів коректурної проби. Завдання полягає в тому, щоб визначити, чи буде зменшуватися кількість помилок уваги у молодших школярів після спеціальних корекційних вправ.
Для вирішення цього завдання психолог у 19 дітей визначає кількість помилок при виконанні коректурної проби до і після корекційних вправ. У табл. 6 наведені відповідні експериментальні дані і додаткові стовпці, необхідні для роботи по парному критерію Т - Вілкоксона.
Зрушення (значення різниці з урахуванням знака)
Абсолютні величини різниць
Ранги абсолютних величин різниць
Символ нетипового двига
Обробка даних за критерієм Т - Вілкоксона здійснюється наступним чином:
У четвертий стовпець таблиці вносяться величини зрушень з урахуванням знака. Їх обчислюють шляхом вирахування з чисел третього стовпчика відповідних чисел другого стовпця.
У п'ятому стовпці у відповідність кожному значенню зсуву ставлять його абсолютну величину.
У шостому стовпці ранжируют абсолютні величини зрушень, представлених в п'ятому стовпці.
За формулою: підраховують суму рангів. У нашому прикладі вона становить:
12,5 + 6,5 + 6,5 + 15 + 16 + 2 + 18 + 17 + 6,5 + 6,5 + 19 + 6,5 + 10,5 + 13,5 + 12 + 6,5 + 13,5 +2 = 190
Перевіряють правильність ранжирування на основі збігу сум рангів отриманих двома способами. У нашому випадки обидві величини збіглися, 190 = 190, отже, ранжування проведено правильно.
Будь-яким символом відзначають всі наявні в таблиці нетипові зрушення. У нашому випадку це три позитивних зрушення.
Підсумовують ранги нетипових зрушень. Це і буде шукана величина. У нашому випадку ця сума дорівнює: = 6,5 + 13,5 + 6,5 = 26,5.
За табл. 15 додатка 6 визначають критичні значення для n = 19.
Потрібна нам рядок табл. 15 з додатка 6 виділена нижче в табл. 7.
Оскільки в нашому випадки основний, типовий зсув - негативний, то додатковий, `` нетиповий '' зрушення буде позитивним і на рівні значущості в 5% сума рангів таких зрушень не повинна перевищувати числа 53, а при рівні значущості в 1% не повинна перевищувати числа 38. Уявімо сказане вище наступним чином:
Будуємо `` вісь значущості '':
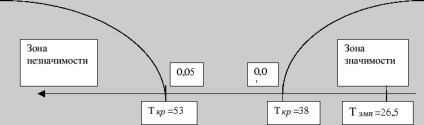
Аналіз `` осі значимості '' показує, що отримана величина Тпопадает в зону значущості. Отже, можна стверджувати, що зафіксовані в експерименті зміни не випадкові і значимі на 1% рівні. Таким чином, психолог може говорити про те, що застосування корекційних вправ сприяє підвищенню точності виконання коректурної проби, отже, робить позитивний вплив на розвиток уваги школярів.
Для застосування критерію Т - Вілкоксона необхідно дотримуватися таких умов:
Вимірювання може бути проведено у всіх шкалах, крім номінальної.
Вибірка повинна бути зв'язковою.
Число елементів в порівнюваних вибірках має бути рівним.
Критерій Т - Вілкоксона може застосовуватися при чисельності вибірки від 5 до 50 (на велику величину не розрахована таблиця достовірності).
У нас можна замовити розв'язання задач з математичної статистики.
А також Ви можете надіслати своє завдання на мою електронну пошту [email protected]