- Визначення. Елементарна кон'юнкція До називається импликантами функції f, якщо для будь-якого набору а = (а1, а2, ..., an) з 0 і 1 умова К (а) = 1 тягне f (a) = 1.
- Определеніе.Імплікант До функції f називається простим. якщо вираз, що виходить з нього викиданням будь-яких множників, вже не импликант функції f.
- Всякий импликант функції f є частина функції f.
- Теорема. Будь-яка функція реалізується диз'юнкція всіх своїх простих импликант.
- Визначення Скорочення ДНФ функції f є диз'юнкція всіх простих импликант функції f.
- Затвердження. Будь-яка функція f реалізується своєї скороченою ДНФ.
- Для будь-якої функції, не рівної тотожно нулю, існує єдина скорочена ДНФ.
- Теорема (Куайна). Якщо в СДНФ функції f провести всі операції неповного склеювання, а потім всі операції поглинання і видалення дублюючих членів, то в результаті вийде скорочена ДНФ функції f.
Алгоритм Куайна побудови скороченою ДНФ
1. Отримати СДНФ функції.
2. Провести всі операції неповного склеювання.
3. Провести всі операції поглинання.
Приклад. Мінімізувати функцію f = 1111010010101111.
Рішення.
1. Будуємо таблицю значення для даної функції (табл.). Будуємо СДНФ функції. При цьому складові нумеруем і записуємо в стовпець (табл.).
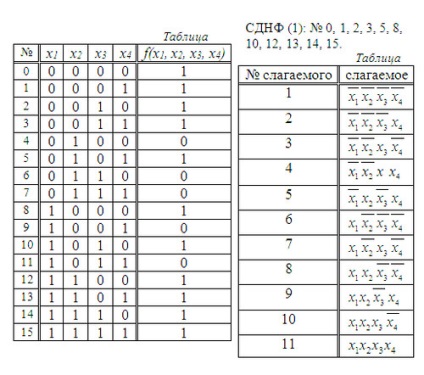
2. Проводимо всі операції неповного склеювання.
Перший етап склеювання (табл.):
У першому етапі склеювання брали участь всі складові СДНФ, значить, ні одна з вихідних доданків не ввійдуть в скорочену ДНФ. Після першого етапу склеювання (і можливих поглинань) отримуємо, що
Пронумеруємо диз'юнктивні члени в отриманої ДНФ в порядку їх слідування від 1 до 15 (табл.).
Другий етап склеювання:
У процедурі склеювання на другому етапі не брали участь складові № 5, 8 з попереднього кроку, тому після другого етапу склеювання і наступних поглинань отримуємо, що
Оскільки подальше склеювання неможливі, то це і буде скорочена ДНФ вихідної функції.