Метод Квайна заснований на виписуванні не всіх можливих кон'юнкція для функції, а тільки тих, які можуть бути присутніми в ДНФ даної функції. При цьому передбачається, що функція задана у вигляді СДНФ. В даному методі елементарні кон'юнкції рангу n, що входять до ДНФ, називаються минтермов рангу n.
Рішення завдання мінімізації булевої функції методом Квайна і вдосконаленим методом Квайна-Мак-Класки базується на поняттях импликант і їх систем.
Алгоритм отримання мінімальної диз'юнктивній нормальної форми МДНФ логічної функції:
1. Логічна функція представляється в СДНФ. Причому, якщо вона задана таблицею істинності, то представляють шляхом запису "по одиницях"; якщо вона задана алгебраїчної довільній диз'юнктивній формі - шляхом застосування операцій розгортання, формул Де Моргана та ін.
2. В отриманому СДНФ проводять всі можливі операції неповного склеювання і потім поглинання. В результаті отримують скорочену діз'юнктівную нормальну форму, тобто диз'юнкцію найкоротших з усіх можливих елементарних творів (прості імпліканти), що входять в дану логічну функцію.
Нехай задана функція представлена в СДНФ. Перехід до скороченій формі заснований на послідовному застосуванні двох операцій: операції склеювання і операції поглинання.
Для виконання операції склеювання в вираженні виявляється пара членів виду і. розрізняються лише тим, що один з аргументів представлений в одному з членів без інверсії, а в іншому - з інверсією. Потім проводиться склеювання таких пар членів:. і результати склеювання вводяться в вираз функції в якості додаткових членів. Далі проводиться операція поглинання. Вона заснована на вираженні: (член поглинає). При поведінці цієї операції з логічного виразу викреслюються всі члени, що поглинаються членами, введеними в вираз в результаті операції склеювання. Операції склеювання і поглинання виконуються послідовно доти, поки це можливо.
3. Знаходять мінімальні диз'юнктивні нормальні форми (МДНФ) по импликантной матриці.
Импликантной матриця - це таблиця, на вертикальні і горизонтальні входи якої записують відповідно члени СДНФ і прості імпліканти заданої логічної функції.
Клітини импликантной матриці, утворені перетином рядків з импликантами і стовпців з поглощательная ними членами СДНФ, відзначають хрестиками [5].
МДНФ знаходять як диз'юнкцію мінімального числа импликант, які спільно накривають хрестиками всі колонки импликантной матриці.
Приклад 4.1. Мінімізувати логічну функцію:
Рішення: 1. Функція задана в алгебраїчній формі, застосовуючи операції розгортання
отримують СДНФ, що містить шість членів:
2. Операції склеювання проводять в наступному порядку:
1) виконуються всі можливі склеювання 1-ого члена з іншими;
2) виконуються всі можливі склеювання 2-ої члена з іншими, крім 1-ого;
3) виконуються всі можливі склеювання 3-ого члена з іншими, крім 1-ого і другого і т.д.
Склеюватися можуть тільки ті члени, у яких число змінних з запереченнями відрізняється на одиницю.
Результати склеювання і поглинання:
Зірочками відзначають ті члени СДНФ, які поглинаються творами, які виникли після склеювання.
У розглянутому прикладі поглинаються всі шість вихідних членів, тому СДНФ заданої функції має вигляд:
До цього виразу операції склеювання і поглинання застосувати не можна, і, отже, воно є скороченою диз'юнктивній нормальною формою логічної функції, а його члени - простими импликантами.
3. Будують для заданої функції импликантной матрицю (табл.4.1.).
Прості імпліканти (минтермов)
Для отримання МДНФ необхідно знайти мінімальне число импликант, які спільно накривають хрестиками всі стовпці импликантной матриці:
Складність логічної функції визначається числом змінних входять до її вираження: в заданій функції 14, в мінімальної - 9.
Перший алгоритм отримання мінімальної кон'юктивний нормальної форми (МКНФ) логічної функції:
1. Логічний функцію представляють в СКНФ. Причому, якщо вона задана таблицею істинності, то її записують "по нулях"; якщо вона задана алгебра в довільній кон'юнктівной формі, то для запису в СКНФ виконують всі можливі операції розгортання.
2. В отриманій СКНФ виконують всі можливі операції неповного склеювання і потім поглинання. В результаті отримують скорочену кон'юнктівную нормальну форму, члени якої є простими макстермамі.
3. МКНФ знаходять по макстермной матриці.
Приклад 4.2. Логічна функція задана таблицею істинності. Знайти МКНФ цієї функції.
5. МКНФ логічної функції:.
Другий алгоритм отримання МКНФ логічної функції:
1. Логічна функція представляється в СДНФ заданої функцією, взятої з запереченням.
Якщо функція задана таблицею істинності, то виписують ряд творів усіх аргументів і з'єднують їх знаками диз'юнкції; кількість творів має дорівнювати числу наборів, на яких задана функція звертається в нуль; під кожним твором записують набір аргументів, на яких функція дорівнює нулю, і над аргументами, рівними нулю, ставлять знаки заперечення.
Якщо функція задана алгебра в довільній формі, то спочатку знаходять її СДНФ, а потім записують диз'юнкцію всіх творів аргументів, які не ввійшли в СДНФ.
2. Знаходять МДНФ по розглянутому вище алгоритму.
3. Від отриманої МДНФ беруть заперечення і, після перетворень за формулами Де Моргана, отримують МКНФ.
Приклад 4.3. Знайти МКНФ, функції заданої таблицею істинності.
3. МДНФ, взята з запереченням:
4. Взявши від обох частин останнього рівності заперечення і застосувавши формулу Де Моргана, отримують МКНФ логічної функції:
У методі Квайна є одна істотна незручність, пов'язане з необхідністю повного по парного порівнювання минтермов на етапі побудови скороченою. ДНФ. У 1956 р Мак - Класки припустив модернізацію першого етапу методу Квайна, що дає істотне зменшення кількості порівнянь минтермов [17].
Ідея методу Мак - Класки полягає в наступному. Все минтермов записуються у вигляді двійкових номерів, наприклад, як 1010. Ці номери розбиваються на групи по числу одиниць в номері, т. Е. В i- ї групи потрапляють номери, які мають в своєму записі i одиниць. Попарне порівняння проводиться тільки між сусідніми по номеру групами, тому що минтермов, придатні для склеювання, відрізняються один від одного тільки в одному розряді. При утворенні минтермов з рангу вище нульового, в розряди, відповідні виключеним змінним, ставиться тире.
Метод передбачає наступну послідовність дій для отримання скороченою ДНФ.
1. Знаходження первинних импликант. Проглядається послідовно кожен минтерм функції і проводиться операція склеювання його з усіма минтермов, з якими це можливо. В результаті склеювання минтермов n- го рангу, виходять минтермов (n -1) -га рангу. Минтермов n-го рангу, які брали участь в операції склеювання, позначаються, наприклад зірочкою. Потім розглядаються минтермов (n -1) -го рангу і до них застосовується операція склеювання. Помечются склеюються минтермов (n -1) -го рангу, записуються отримані в результаті склеювання минтермов (n -2) -го рангу і т.д. Етап закінчується, якщо знову отримані минтермов l -го рангу вже не склеюються між собою. Все невідмічені минтермов називаються первинними импликантами. Їх диз'юнкція являє собою скорочену ДНФ функції.
Потім склеюються минтермов четвертого рангу і знову склеюються минтермов позначаються зірочками:
Утворюються минтермов другого рангу:
Первинними (простими) импликантами є:
2. Розстановка позначок. Для даної функції скорочена ДНФ має вигляд:
Для побудови тупикових ДНФ і Сокр. ДНФ потрібно викинути зайві інтервали. Будується таблиця, рядки якої відповідають первинним импликантами, а стовпці - минтермов СДНФ. Якщо в деякий з минтерм входить якийсь із импликант, то на перетині відповідного рядка і стовпця ставиться мітка.
3. Знаходження істотних импликант. Якщо в будь-якому стовпці міститься тільки одна одиниця, то первинна импликанта, що визначає цей рядок, називається суттєвою. Наприклад, істотною импликантой є. Істотна импликанта не може бути видалена з Сокр. ДНФ, тому що тільки вона здатна покрити деякі минтермов СДНФ. Тому з таблиці виключаються рядки, які відповідають цим импликантами, і стовпці, що мають одиниці в цих рядках.
У розглянутому прикладі виключається рядок і стовпці
В результаті отримуємо таблицю:
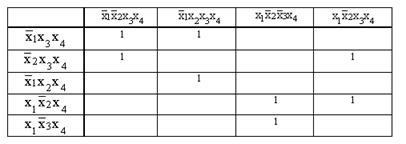
4. Викреслювання зайвих стовпців і рядків. Якщо в отриманій таблиці є однакові стовпці, то викреслюються всі, крім одного. Якщо після цього в таблиці з'являться порожні рядки, то вони також викреслюються.
5. Вибір мінімального покриття максимальними інтервалами. В отриманій таблиці вибирається така сукупність рядків, яка містить одиниці у всіх шпальтах. При декількох можливих варіантах такого вибору, перевага віддається варіанту з мінімальним числом букв в рядках, що утворюють покриття. Мінімальне покриття таблиці утворюють рядки, відповідні импликантами. Тоді МДНФ має вигляд:
Приклад 4.4. Провести мінімізацію функції, заданої таблично.
Попарним порівнянням членів (кожного з членів з усіма посліду-ющими) виявляємо склеюються пари членів:
1-й і 4-й члени (результат склеювання)
2-й і 3-й члени (результат склеювання)
2-й і 4-й члени (результат склеювання)
3-й і 5-й члени (результат склеювання)
4-й і 5-й члени (результат склеювання)
Результати операції склеювання вводимо в вираз функції і проводимо операцію поглинання ними членів вихідного вираження:
Повторюємо операції склеювання і поглинання.
Тут операція склеювання проводиться з двома парами: і. і. і подальше склеювання неможливо, це є скороченою формою (а в даному прикладі і мінімальної формою)
У даній функції і є простими импликантами