Мінімізація логічних функцій методом Квайна
Метод Куайна - спосіб представлення функції в ДНФ або КНФ з мінімальною кількістю членів і мінімальним набором змінних. [1] [2] [3]
Перетворення функції можна розділити на два етапи:
- на першому етапі здійснюється перехід від канонічної форми (СДНФ або СКНФ) до так званої скороченою формі;
- на другому етапі - перехід від скороченої форми до мінімальної формі.
Перший етап (отримання скороченою форми)
Уявімо, що задана функція представлена в СДНФ. Для здійснення першого етапу перетворення проходить два дії:
Операція склеювання зводиться до знаходження пар членів, що відповідає виду або, і перетворенню їх в такі вирази:. Результати склеювання w тепер грають роль додаткових членів.
Потім виконується операція поглинання. Вона заснована на рівності (член поглинає вираз). В наслідок цього дії з логічного виразу викреслюються всі члени, що поглинаються іншими змінними, результати яких отримані в операції склеювання.
Обидві операції першого етапу можуть виконуватися до тих пір, поки це може бути здійснено.
Застосування цих операцій продемонстровано в таблиці:
Результат операції склеювання потрібен для перетворення функції на другому етапі (поглинання)
Членами результату склеювання є
Член поглинає ті члени вихідного вираження, які містять, тобто перший і четвертий. Ці члени викреслюються. Член поглинає другий і третій, а член - п'ятий член вихідного вираження.
Повторення обох операцій призводить до наступного виразу:
Тут склеюється пара членів і (склеювання пари членів і призводить до того ж результату), результат склеювання поглинає 2-, 3-, 4-, 5-й члени виразу. Подальше проведення операцій склеювання і поглинання виявляється неможливим, скорочена форма вираження заданої функції (в даному випадку вона збігається з мінімальною формою)
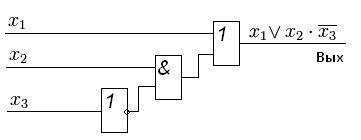
Структурна схема функції
Члени скороченою форми (в нашому випадку це і) називаються простими импликантами функції. У підсумку, ми отримали найбільш простий вислів, якщо порівнювати його з початковою версією - СДНФ. Структурна схема такого елемента показана на малюнку справа.
Другий етап (отримання мінімальної форми)
Як і на першому етапі, в отриманому рівність можуть міститися члени, усунення яких ніяким чином не вплине на кінцевий результат. Наступний етап мінімізації - видалення таких змінних. Таблиця, подана нижче містить значення істинності функції, по ній буде зібрана наступна СДНФ.
СДНФ. зібрана по цій таблиці виглядає наступним чином:
Кінцеве вираз досягається зарахунок повторного використання операцій склеювання і поглинання:
Члени цього виразу є простими импликантами вираження. Перехід від скороченою форми до мінімальної здійснюється за допомогою импликантной матриці.
Члени СДНФ заданої функції вписуються в стовпці, а в рядки - прості імпліканти, тобто члени скороченою форми. Відзначаються стовпці членів СДНФ. які поглинаються окремими простими импликантами. У наступній таблиці проста импликанта поглинає члени і (в першому і в другому шпальтах поставлені хрестики).
импликантной матриця
Друга импликанта поглинає перший і третій члени СДНФ (вказано хрестиками) і т. Д. Импликантами, що не підлягають виключенню, утворюють ядро. Такі імпліканти визначаються за вищевказаною матриці. Для кожної з них є хоча б один стовпець, що перекривається тільки цієї импликантой.
У нашому прикладі ядро складають імпліканти і (ними перекриваються другої та шостої стовпці). Виняток з скороченою форми одночасно всіх импликант, що не входять в ядро, неможливо, так як виключення однієї з импликант може перетворити іншу в уже незайве член.
Для отримання мінімальної форми досить вибрати з импликантами, що не входять в ядро, таке мінімальне їх число з мінімальною кількістю букв в кожному з цих импликант, яке забезпечить перекриття всіх стовпців, що не перекритих членами ядра. У розглянутому прикладі необхідно импликантами, що не входять в ядро, перекрити третій і четвертий стовпчики матриці. Це може бути досягнуто різними способами, але так як необхідно вибирати мінімальне число импликант, то, очевидно, для перекриття цих стовпців слід вибрати імліканту.
Мінімальна діз'юнктівная нормальна форма (МДНФ) заданої функції:
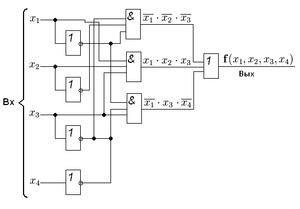
Натисніть на зображення для його збільшення
Структурна схема, що відповідає цьому виразу приведена на малюнку зліва. Перехід від скороченою схеми до МДНФ був здійснений шляхом виключення зайвих членів - импликант і. Покажемо допустимість подібного винятку членів з логічного виразу.
Імпліканти і стають рівними лог. 1 відповідно при наступних наборах значень аргументів: = 0, = 0, = 0 і = 1, = 1, = 0.
Роль цих импликант в вираженні скороченою форми функції полягає лише в тому, щоб на приведених наборах значень аргументів привласнювати функції значення 1. Однак при цих наборах функція дорівнює 1 через інших импликант вираження. Дійсно, підставляючи набір значень, зазначених вище в формулу (а). отримуємо:
- при = 0, = 0, = 0
;
- при = 1, = 1, = 0
;
Використання методу для отримання мінімальної КНФ
Для отримання Мінімальною кон'юнктивна нормальна форма (МКНФ), використовуючи метод Куайна, вводяться слудующие критерії:
- для мінімізації береться НЕ СДНФ. а СКНФ функції;
- склеюються пари членів змінюються на: або;
- правило операції поглинання виглядає наступним чином: