Кривизна пласкою кривою. Радіус кривизни. Еволюта і евольвента плоскої кривої


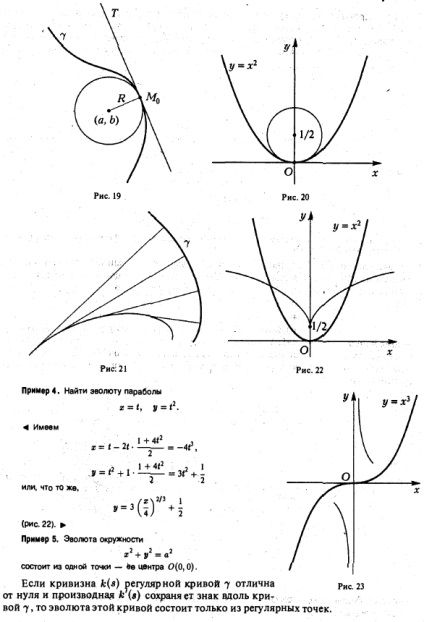





Нехай 7 - регулярна крива і Af0 - точка цієї кривої. Визначення. Кривизною до кривої 7 в точці М0 називається межа відносини при - найменший кут між дотичними до кривої 7 в точках - довжина дуги ^ М0М (рис. 16). Кривизна кривої характеризує швидкість її откл Онен від дотичній. Кривизна прямий дорівнює нулю в кожній її точці. Кривизна кола постійна і дорівнює j, де - радіус кола. 2-регулярна крива має в кожній своїй точці певну кривизну. Якщо - природна параметризація кривої 7, то її кривизна може бути знайдена за формулою 6 випадку довільної параметризації Кривизна плоскої кривої. Радіус кривизни. Еволюта і евольвента плоскої кривої Наочний спосіб освіти евольвенти Просторові криві. Способи завдання При явному способі завдання Приклад 1. Кривизна параболи у = г1 в її вершині 0 (0,0) дорівнює 2. Кривизна плоскої кривої за визначенням неотрицательна. Однак у багатьох ^ y4a # v кривизни плоскої кривої корисно віднести знак. Зазвичай вибір знака зв'язок-ваютс ПАПР ° ням обертання дотичної до кривої при переміщенні уздовж кривої при зростанні параметра: «4»: кривизна кривої позитивна, якщо дотична обертається проти годинникової стрілки (в позитивному напрямку); «-»: кривизна кривої негативна, якщо дотична обертається за годинниковою стрілкою (в негативному напрямку) (рис. 17). шсдосрмвіе на явно заданої кривої обчислюють за 'Прмір 2. Кривизна сінусоіАи у = sin г поклади тельнв (дорівнює 1) вточ * е J, -l) і негативна (дорівнює -1) в точів l) (рис. 18). У точці про іріеіена сінуахд * рвана нулю. Якщо кривизна кривої в точці Мо (* о) відмінна від нуля, то визначено рідне кривизни кривої в цій точці Про Окружність радіуса R (to), що проходить через точку Afb (fo), що має в цій точці з кривою 7 про- рнс.18 шую дотичну і лежащия а поту ж сторону від цієї дотичної, що і крива 7, називаєте я дотичної окружністю кривої 7 в точці Afo, або колом кривизни (рис. 19). Ясно, що кривизни кривої і її окружності кривизни в їх спільній точці збігаються. Центр стикалися-щейсяокружності називаючи ється центром кривизни кривої в точці Af0. Його координати а і b обчислюються за формулами • Приклад 3. Для параболи у = х2 в її вершина 0 (0,0) маємо Я »j, в = 0. Поетом у коло кривизни параболи в точев Про може бути задана уратежем (рис.20). Еволюта регулярної плоскої кривої називаєте я безліч її центро в кривий нзни (рис. 21). Рівняння еволюти кривої 7, заданої параметрично, мають такий вигляд: Знайти еволюта параболи Приклад 5. Еволюта окружності складається з однієї точки - її центру 0 (0,0). Якщо кривизна регулярної кривої 7 відмінна від нуля і похідна до (s) збережи ет знак уздовж кривої 7, то еволюта цієї кривої складається тільки з регулярних точок. Якщо кривизна k (s) регулярної кривої 7 дорівнює нулю в деякій точці кривої, k (so) = 0, а її похідна зберігає знак уздовж кривої 7, то еволюта цієї кривої розпадається на дві регулярні криві, що є еволюта частин кривої 7 при s Кожна з цих гілок йде в нескінченність при s -> sq. Приклад в. Кривизна параболи у = х2 в її вершині 0 (0,0) відмінна від нуля, а похідна кривизни 2 цієї статті не зберігає знака вздовж параболи. Тому еволюта параболи і має особливість - точку повернення першого роду (див. Рис. 22). Приклад 7. Кривизна кубічний параболи у = х3 Кривизна плоскої кривої. Радіус кривизни. Еволюта і евольвента плоскої кривої Наочний спосіб освіти евольвенти Просторові криві. Способи завдання при х = Q звертається в нуль, а її похідна в околиці точки 0 (0,0) зберігає знак. Тому еволюта кубічної параболи розпадається на дві регулярні гілки (рис. 23). / Евольвент кривої 7 називається крива, для якої дана крива 7 є еволюта. Евольвента кривої 7 збігається з безліччю кінців відрізків дотичних до кривої 7, відкладених від точок дотику, довжини яких зменшуються на величину, рівну приросту дуги кривої 7. Наочний спосіб освіти евольвенти Відкладемо на кривій 7 від іроізвольной точки Мо цієї кривої дугу довжини с. Позначимо другий кінець дуги через Af. Уявімо тепер, що на дугу ^ mqm накладена гнучка нерозтяжна нитка, один з кінців якої закріплений в точці mq. При змотуванні натягнутою нитки з кривою 7 (як з шаблону) другий її кінець М опише евольвенту кривої 7 (рис. 24). де с - довільна постійна. Тим самим, у будь-який регулярної кривої існує нескінченне число евольвент. Приклад 8. евольвент окружності описуються рівняннями виду де с - параметр сімейства евольвент (рис. 25). § 3. Просторові криві. Способи завдання Onptделеніе. Параметрично заданої просторової кривої називається безліч 7 точок М, координати х, у і г яких визначаються співвідношеннями де - функції, безперервні на відрізку [а, Ь), або у векторній формі г, де Наочно параметрически задану криву можна представляти какслед рухається точки М з координатами. Приклад 1. 'рівняння дау »« ітко * гвинтовий ліміі (рис.27). Т'чкі А і Л кривої 7, Відповідальні значенням t = а і t = 6 параметра відповідно, називаються початковим і кінцевим пунктом кривої у. Крива 7 називається зо-мкнутой, якщо ці точки співпадають. Поняття гладкою і регулярної просторової кривої вводяться в повній відповідності з плоским випадком: крива 7, задана параметричних векторних рівнянням s називається п-регулярної, якщо 1) векторна функція г (() має на відрізку [а, Ь) безперервні похідні порядку п і 2 ) швидкість кривої пайЬжітельна в каж ^ бй ^ очку. Іншим поширеним способом завдання просторової кривої є неявний спосіб завдання кривої як безлічі точок М, координати х, у і z яких є рішенням системи рівнянь де функції) підкоряються певним умовам. Зазначимо важливий окремий випадок, найбільш часто зустрічається на практиці: z) є гладкими функціями своїх аргументів і в деякій точці виконані умови: Неявно задана просторова крива, в кожній точці которо й виконується умова (3), буде регулярною. Приклад 2. Крим, мдамша * уронвніямі буде регулярною (рис.28). Ця Крим предсташліет собою велику окружність - про> ч * НЙ »сфери площиною, викладач * -щей * вр * е її центр. Нехай 7 - регулярна крива, задана параметрично. Позначимо через Мо точку кривої 7, що відповідає значенню to параметра, а через М - точку кривої, що відповідає значенню t з деякої околиці * о »Пряма MqT називається дотичній до кривої 7 в точці Мо, якщо при М -" Мо найменший з кутів АТ між цієї прямої і змінної прямої М0М Рис. 2s прагне до нул ю. Регулярна крива імееткасател ьіую в кожній своїй точці. Вектор швидкості кривої в точці М0 коллінеарен її дотичне ой в цій точці. Рівняння дотичної до кривої 7 в точці Мо (®е »Уо,« о) мають такий вигляд Будь-яка пряма, що проходить через точку Щ перпендикулярно дотичній до кривої 7 в точці М0, називається нормаллю кривої 7 в точці Мо. Площина / Що проходить через точку М0 кривої 7 перпендикулярно її дотичній MoT в цій точці, називається нормальної площиною кривої в точці Мо (рис. 29). Рівняння нормальної площині кривої, заданої параметрично, має такий вигляд: Ясно, що все нормалі кривої в точці Мо лежать в її нормальної площини в цій точці. Приклад 3. Дотична і нормальна площина гвинтовий лінії в точці ^, (при t = j) описуються рівняннями відповідно. Регулярна просторова крива спрямляема. Довжина кривої, заданої векторних рівнянням обчислюється за формулою В разі координатного завдання кривої Кривизна плоскої кривої. Радіус кривизни. Еволюта і евольвента плоскої кривої Наочний спосіб освіти евольвенти Просторові криві. Способи завдання маємо Значення функції дорівнює довжині дуги кривої 7, укладеної між точками А (а) і M (t) (рис. 30). Ця функція строго зростає на відрізку [о, Ь), причому Тим самим, довжину дуги можна взяти за новий параметр на кривій. Параметризація кривої, де в якості параметра взята довжина дуги з, називається природною параметризацією. Крива з природною параметризацією має одиничну швидкість (Ьтносітельно цієї параметризації). Для того, щоб параметризация кривої була природною, необхідно і достатньо виконання умови або, що те ж саме, Приклад 4. Для гвинтової лінії маємо Тому природна параметризація гвинтовий лінії може бути записана так