Кути і сторони в трикутниках, математика

85. Побудуємо рівнобедрений ΔABC (чер. 92), у якого AB = BC. Тоді ми знаємо, що його кути при основі рівні, т. Е. ∠A = ∠C. Пронумеруємо ці кути, - тоді ∠1 = ∠2. Станом тепер будувати нові трикутники ABC ', ABC' 'і т. Д. Так, щоб сторона AB і ∠B залишалися незмінними, але сторона BC збільшувалася. Тоді кут A повинен збільшуватися (що очевидно), а кут C стане зменшуватися: ми бачимо, що ∠3 <∠2, ∠4 <∠3 и т. д. потому что ∠2 есть внешний угол для ∆ACC' и, следов. ∠2> ∠3 або ∠3 <∠2, также ∠3 есть внешний угол ∆AC'C'' и, след. ∠3> ∠4 або ∠4 <∠3 и т. д. (уменьшение угла C видно еще из того, что сумма углов треугольника всегда равна 2d: угол B не изменяется, угол A увеличивается, – след. ∠C должен уменьшаться).

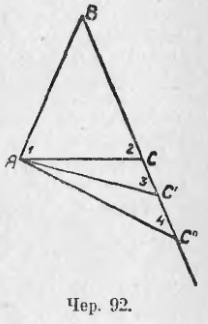
З цих побудов ми маємо право зробити висновки:

1) Якщо в трикутнику дві сторони рівні, то проти них лежать рівні кути.

2) Якщо в трикутнику дві сторони не рівні, то проти більшої з них лежить і більший кут.

86. Тепер, навпаки, побудуємо: 1) трикутник з двома рівними кутами і 2) трикутник з двома нерівними кутами і порівняємо боку, протилежні цим кутах. Для вирішення питань, тут виникають, скористаємося способом міркування, часто вживаним в математиці.

1) Нехай ΔABC (чер. 93) постоїв так, що ∠A = ∠C. Порівняти боку BC і BA.

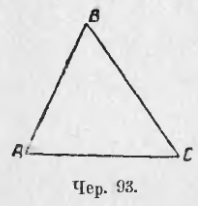
Поки, не знаючи нічого про боку AB і BC, ми можемо зробити про них 3 припущення: 1) AB = BC, 2) AB> BC і 3) AB BC має, на підставі попереднього п. Спричинити за собою наслідок, що ∠C> ∠A, а у нас побудовано: ∠C = ∠A. Отже, це припущення має бути викреслено. Також з 3-го припущення, що AB ∠C, що також суперечить нашому побудови. Отже, і це припущення має бути викреслено. Залишається тому лише одне припущення, що AB = BC, яке і повинно бути вірно, так як інших зробити не можна. Тому маємо:

Якщо в трикутнику два кути рівні, то проти них лежать рівні сторони.

2) Нехай ΔABC (чер. 93) постоїв так, що ∠A> ∠C. Порівняти боку BA і BC.
Знову ми можемо зробити 3 припущення: 1) AB = BC, 2) AB> BC і 3) AB BC не годиться, так як з нього випливало б, що ∠C> ∠A, що суперечить побудові. Залишається лише 3-е припущення, що AB

Якщо два кути в трикутнику нерівні, то проти більшого з них лежить велика сторона.

Тепер легко вирішуються питання: 1) яка зі сторін прямокутного трикутника найбільша? 2) Яка зі сторін тупоугольного трикутника найбільша?

87. У двох попередніх пп. ми мали справу з двома положеннями: 1) проти більшої сторони лежить більший кут і 2) проти більшого кута лежить більша сторона. Ми знайшли, що ці думки справедливі для одного трикутника. Виникає питання, чи справедливі вони для двох трикутників. Безсумнівно справедливі для двох рівних трикутників. так як рівні трикутники можна накладенням злити в один трикутник. Але, взагалі кажучи, до двох різних (не рівним) трикутниках ці положення не можуть бути застосовні: ми можемо побудувати два таких трикутника ΔABC і ΔA'B'C '(чер. 94), щоб ∠B був> ∠B' , але AC була б

Цей випадок легко усвідомлюється наочно. Візьмемо дві палички AB і BC (чер. 95 bis) і складемо їх кінцями (в точці B). Якщо обертати паличку BC близько точки B по стрілці, то ∠B стане збільшуватися: сторона BC буде змінювати своє положення (нехай одне з них є BC '), але весь час BC залишиться рівним самому собі; не змінюється також і відрізок AB. Звернемо увагу, що точками A і C визначається ще відрізок AC, на кресленні не зображений. При вищевказаному обертанні точка C змінює своє місце і нам ясно, що цей відрізок AC, чи не зображений на кресленні, повинен збільшуватися (напр. AC '> AC), т. Е. Якщо 2 сторони трикутника не змінюються, а кут між ними збільшується, то третя сторона так само збільшується. У тексті цей випадок з'ясований без допомоги такого наочного уявлення.

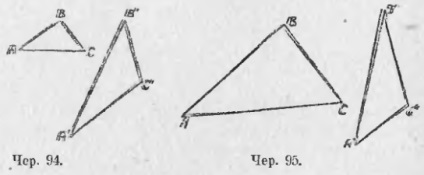
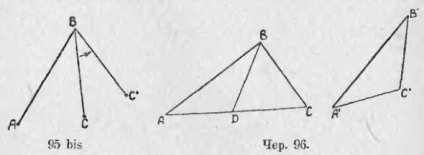
Побудуємо два таких трикутника, щоб у них було по дві рівних боку, але щоб кути між ними не були рівні. Нехай в ΔABC і в ΔA'B'C '(чер. 95) маємо AB = A'B', BC = B'C ', але ∠B> ∠B'. Порівняємо боку AC і A'C ', що лежать проти нерівних кутів. Для цього накладемо ΔA'B'C 'на ΔABC так, щоб сторона A'B' збіглася з рівною їй стороною AB. Тоді сторона B'C 'повинна піти всередині ∠B, тому що ∠B' <∠B, но где кончится эта сторона, т. е. где расположится точка C', неизвестно. Может быть, она расположится как раз на стороне AC, может быть, расположится вне ∆ABC, а может быть внутри этого треугольника. Разберем эти три случая отдельно.

1) Нехай ΔA'B'C 'розташується так, що займе положення ΔABD (чер. 96), так що точка C' потрапить в D, на сторону AC; тоді, очевидно, AD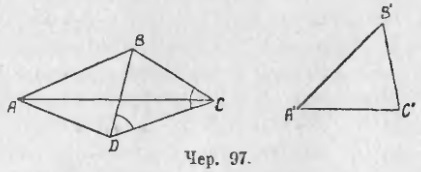

2) Нехай ΔA'B'C 'при накладенні займе положення ΔABD (чер. 97), т. Е. Точка C' розташується в точці D, поза ΔABC. Тоді, з'єднавши точки C і D, отримаємо ΔBCD, у якого BC = BD, так як, за побудовою, B'C '= BC, а BD є та ж сторона B'C', лише перенесена в інше місце. Тому ΔBCD - рівнобедрений, і ∠BCD = ∠BDC. Розглянемо тепер ΔACD; про два його кута, а саме про ∠C (або ∠ACD) і про ∠D (або ∠ADC) легко збагнути, користуючись зазначеними рівними кутами рівнобедреного трикутника, який з них більше іншого. Справді, ми бачимо, що ∠ACD <отмеченного угла BCD при основании равнобедренного треугольника, а ∠ADC> зазначеного кута BDC при підставі рівнобедреного трикутника. Але ∠BCD = ∠BDC, отже, ∠ADC> ∠ACD. Тому на підставі п. 86 (застосовуючи його до ΔACD) маємо AC> AD, але AD є сторона A'C ', перенесена в інше місце, - отже, AC> A'C'.

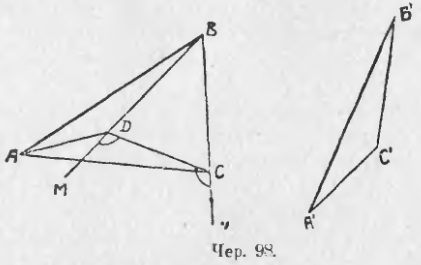
3) Нехай ΔA'B'C 'при накладенні займе положення ΔABD (чер. 98), т. Е. Точка C' розташується усередині ΔABC. Тоді, з'єднавши точки C і D, отримаємо рівнобедрений ΔCBD (BD = BC, бо BD є сторона B'C ', перенесена в інше положення, а B'C' = BC з побудови) і, отже, ∠BCD = ∠BDC . Якщо продовжити боку BD і BC за напрямками DM і CN, то отримаємо два зовнішніх кута цього рівнобедреного трикутника ∠MDC і ∠NCD, але ∠MDC = ∠NCD, отже, ∠ADC> ∠ACD, а тому, на підставі п. 86, маємо AC> AD, або AC> A'C '(AD є сторона A'C', перенаправлення в інше положення).

Отже, у всіх трьох випадках виявилося, що

т. е. якщо дві сторони одного трикутника відповідно дорівнюють двом сторонам другого трикутника, але кути між ними не рівні, то проти великого кута лежить більша сторона.

88. Розберемо зворотний питання. Нехай побудовані ΔABC і ΔA'B'C '(чер. 95) так, що AB = A'B', BC = B'C ', але AC> A'C', т. Е. Два трикутника мають по дві рівних боку, але треті сторони їх не рівні. Порівняти ∠B і ∠B '.
Скористаємося тим же способом міркування, як в п. 86.

Поки ми можемо про кути B і B 'зробити три припущення: 1) ∠B = ∠B', 2) ∠B> ∠B 'і 3) ∠B <∠B'.

Перше припущення не годиться, так як тоді наші трикутники, маючи з побудови по дві рівних боку і рівні кути між ними, були б рівні, і, отже, AC '= A'C', а це суперечить побудові. Третє припущення, що ∠B <∠B' также не годится, так как тогда к этим треугольникам был бы применим результат, найденный в предыдущем п. на основании которого имели бы AC ∠B ', яке і повинно бути вірно. Отже:

Якщо дві сторони одного трикутника дорівнюють відповідно двом сторонам іншого, але треті сторони цих трикутників не рівні, то проти більшої сторони лежить і більший кут.