Результати вимірювання діаметра капіляра заносяться в таблицю 4.2, інших вимірів - в таблицю 4.3.
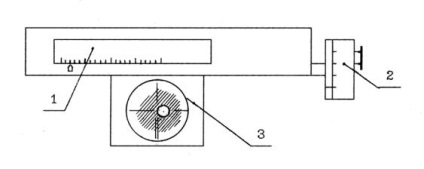
4.5.1 Виміряти за допомогою мікроскопа діаметр капіляра. Для цього зріз капіляра помістити на предметне скло мікроскопа. Поєднати візирні лінії окуляр-мікрометра з правим, а потім з лівим краями отвору капіляра, як на малюнку 4.4. Зняти відлік по горизонтальній шкалою (цілі міліметри) і за шкалою барабана (десяті і соті частки міліметра). Знайти діаметр капіляра як різниця цих відліків. Діаметр капіляра виміряти в трьох різних напрямках. За діаметр капіляра прийняти середнє арифметичне отриманих результатів. Обчислити радіус R капіляра.
4.5.2 За допомогою терезів визначити масу m 1 порожнього стакана 4 з точністю до 0,01 г.
4.5.3 Виміряти лінійкою початкову висоту рівня рідини h 'від площини стола.
1 - горизонтальна шкала; 2 - шкала барабана; 3 - поле зору мікроскопа Малюнок 4.4 - Схема вимірювання діаметра капіляра
4.5.4 Швидко опустити капіляр з положення А в положення В (див. Рисунок 4.3), так щоб рідина стікала в стакан 4 і включити секундомір.
4.5.5 Виміряти висоту h кінця капіляра від площини стола.
4.5.6 Коли рідини в склянці 4 буде досить (1/2 обсягу), вимкнути секундомір, швидко піднявши при цьому капіляр в положення А. Вважати з секундоміра час витікання рідини t.
4.5.7 Виміряти кінцевий рівень рідини h '' в посудині 1.
4.5.8 Визначити масу m 2 склянки з рідиною.
4.5.9 Занести в таблицю 4.3 значення: прискорення сили тяжіння
(G = 9,8 м / с 2), щільності рідини (ρ води = 10 3 кг / м 3) і довжину капіляра, значення якої вказано на установці.
5 Визначення модуля Юнга по деформації розтягування
Мета роботи - вивчення поведінки деформівних тіл при дії на них зовнішніх сил і експериментальне визначення модуля Юнга по деформації розтягування.
5.2 Теоретичне введення
У теоретичної механіки (статики) вивчається рівновага абсолютно твердого тіла; цього подання про матеріал досить для вирішення поставленого в статиці завдання - визначення умов, при яких можливе взаємне урівноваження прикладених до тіла сил. При вивченні опору матеріалів дії цих сил такого грубого наближеного уявлення про властивості матеріалу вже недостатньо; ми повинні врахувати, що абсолютно твердих тіл в природі не існує.
Насправді тіла під дією прикладених до них сил в тій чи іншій мірі змінюють свою форму і розміри, тобто деформуються. Величини і характер деформацій пов'язані зі структурою, будовою застосовуваних нами матеріалів. Всі ці матеріали можуть бути розбиті на два класи: кристалічні і аморфні [1].
Кристалічні матеріали складаються з величезної кількості хаотично розташованих відносно один одного дрібних кристаликів. Відомо, що в окремому кристалі (монокристали) атоми розташовуються в певному порядку, утворюючи кристалічну решітку. Кристалічну структуру мають метали (полікристалічні тіла). В аморфних тілах (скло, смоли і т.п.) на відміну від кристалів немає строгого порядку в розташуванні атомів. Тільки найближчі атоми-сусіди розташовуються в деякому порядку. Але суворої повторюваності у всіх напрямках одного
і того ж елемента структури, яка характерна для кристалів, в аморфних тілах немає.
Атоми утримуються в рівновазі силами взаємодії. Деформація тіл відбувається за рахунок зміни розташування атомів, їх зближення або видалення. Деформації поділяються на пружні і пластичні. Пружними деформаціями називаються такі зміни форми і розмірів елементів, які зникають після видалення викликали їх сил, - тіло повністю відновлює свою колишню форму. Ці деформації пов'язані лише з пружними спотвореннями решітки атомів. Досвід показує, що пружні деформації спостерігаються, поки величина зовнішніх сил не перевершила певної межі.
Якщо ж зовнішні сили перейшли цю межу, то в результаті зсуву атоми і молекули змінюють своїх "сусідів" і починають взаємодіяти з
іншими. Після припинення дії зовнішніх сил вони вже не повертаються до попереднього стану, форма і розміри елемента не відновлюються в первісному вигляді. Такі деформації називаються пластичними. Пластичні деформації зберігаються в тілі після зняття навантаження, тому їх ще називають залишковими. У кристалічних матеріалах ці деформації пов'язані з необоротними переміщеннями одних верств кристалічної решітки щодо інших.
Залежно від напрямку дії сил, прикладених до тіла, можуть виникати різні види деформацій: розтяг, стиск, зсув, кручення, вигин. Ми будемо знайомитися з деформацією тіл найбільш простої форми. До таких тіл відносяться так звані призматичні стержні з прямою віссю. Крім того, будемо вважати, що сам стрижень не має маси.
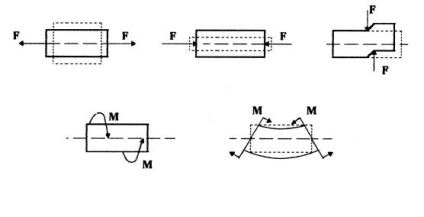
а - розтягнення; б - стиснення; в - зсув; г - кручення; д - вигин Малюнок 5.1 - Види деформацій
Деформація розтягу або стиску виникає в тому випадку, коли зовнішні сили спрямовані по одній прямій (уздовж осі стрижня) в різні боки, як на малюнку 5.1, а, б. Якщо на стрижень діють зовнішні сили, які прагнуть зрушити одну частину його відносно іншої, то виникає деформація зсуву. При цьому, як видно з малюнка 5.1, в, сили утворюють пару з невеликим плечем в площині поздовжньої осі стержня. Якщо стрижень знаходиться під дією навантажень, що створюють протилежні пари сил в площинах, перпендикулярних поздовжній осі стрижня, то з'являється деформація кручення, показана на малюнку 5.1, г. І, нарешті, якщо дві пари сил різного знака діють в площині поздовжньої осі стержня, то створюється деформація вигину, показана на малюнку 5.1, д.
В теорії пружності доводиться, що всі типи деформацій можуть бути зведені (за умови, що вони досить малі) до одночасно відбувається деформацій розтягування (або стискування) і зсуву.
Зсув атомів при деформації матеріалу під дією зовнішніх сил супроводжується зміною сил взаємодії між атомами - сил тяжіння і відштовхування. У всякому твердому тілі під дією зовнішніх сил виникають додаткові внутрішні сили, які супроводжують де-
формацію матеріалу. Ці внутрішні сили чинять опір прагненню зовнішніх сил зруйнувати тіло, змінити його форму, відокремити одну його частину від іншої. Вони прагнуть відновити колишню форму і розміри деформованої частини тіла. Звідси випливає, що для вирішення задач опору матеріалів необхідно перш за все навчитися по зовнішнім силам визначати внутрішні сили пружності. Для цього застосовують метод перетинів. сутність якого полягає в наступному.
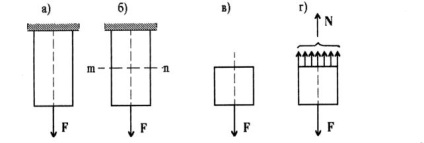
Нехай до кінця однорідного стержня з площею поперечного перерізу S прикладена сила F. діюча на весь переріз стержня рівномірно, інший кінець стрижня закріплений, як показано на малюнку 5.2, а.
Розділимо подумки стрижень на дві частини перетином m-n, перпендикулярним його осі, як на малюнку 5.2, б, і визначимо сили, з якими ці частини стержня діють один на одного. Так як обидві частини стрижня знаходяться в рівновазі, то векторна сума сил, що діють на кожну з них, повинна бути дорівнює нулю. Відкинемо верхню частину і розглянемо рівновагу нижньої (див. Рисунок 5.2, в, г). Рівновага цій частині не порушиться лише в тому випадку, якщо до неї додати реакції - внутрішні сили, які замінять
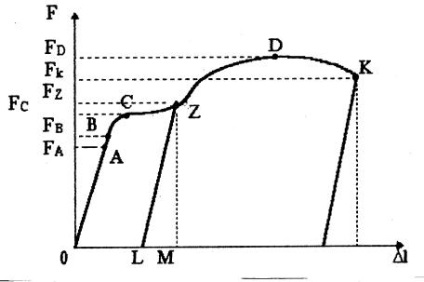
Будь-яке тверде тіло дає деформації, що підкоряються закону Гука лише до певної межі. Розглянемо поведінку матеріалів в досвіді на розтягнення аж до руйнування. Результати вимірювань найбільш наочно можна представити у вигляді так званої діаграми розтягування. При кресленні діаграми по вертикальній осі відкладаються в певному масштабі навантаження, а по горизонтальній - абсолютні подовження. При розтягуванні зразка з пластичного матеріалу (наприклад, маловуглецевої сталі) діаграма має вигляд, показаний на малюнку 5.4.
Прямолінійна ділянка ОА відповідає пружним деформаціям зразка. Ордината F А являє собою величину сили, що розтягує, відповідає межі пропорційності σ П. тобто того найбільшій напрузі, перевищення якого викликає відхилення від закону Гука.
При збільшенні сили, що розтягує за величину F А деформація починає рости швидше навантаження - діаграма має криволінійний вид з опуклістю вгору. Однак до точки В деформації пружні, тобто зразок відновлює свою форму після зняття навантаження. За точкою В з'являються непружні деформації.
Напруга, при перевищенні якого в тілі з'являються залишкові деформації, називається межею пружності σ у; на діаграмі навантаження, що викликає цю напругу, вимірюється ординатою F В.
Точки А і В настільки близькі один одному, що зазвичай беруть межу пружності і межа пропорційності збігаються. Тому часто говорять, що матеріал слід закону Гука, поки не досягне межі пружності, хоча правильніше було б сказати - межі пропорційності.
Малюнок 5.4 - Діаграма розтягування маловуглецевої стали
При деякому значенні сили, що розтягує F з матеріал "тече"; для збільшення деформації майже не потрібно збільшувати розтягувальну силу. На діаграмі утворюється горизонтальна (або майже горизонтальна) майданчик.
Напруга, при якому відбувається такий перебіг матеріалу - зростання деформацій при постійній (приблизно) навантаженні, називається межею плинності σ т.
Після утворення майданчики плинності матеріал знову починає чинити опір подальшому розтягуванню, і для збільшення подовження l доводиться збільшувати силу. Точка D діаграми відповідає найбільшою величиною навантаження.
Якщо зняти навантаження в стані, описуваному деякою точкою Z, що лежить між точками С і D, то при розвантаженні діаграма буде зображуватися прямий ZL, приблизно паралельній прямій ОА. Таким чином, зразок в цьому випадку не повернеться до первісних розмірів; відрізок LM представлятиме пружне подовження, як і раніше мінливий пропорційно навантаженню з колишнім модулем пружності; відрізок OL - залишкове подовження і відрізок ОМ повне подовження при навантаженні F z.
Найбільша величина розтягує стержень сили зображується ординатою F D; вона часто називається руйнівним навантаженням. так як необ-