Теоретична механіка (Статика)
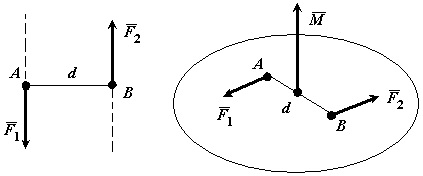
Парою сил називається система двох рівних по модулю, паралельних і направлених в протилежні сторони сил, що діють на абсолютно тверде тіло.
Площиною дії пари сил називається площину в якій розташовані ці сили.
Пліч-о-пари сил d називається найкоротша відстань між лініями дії сил пари.
Моментом пари сил називається вектор, модуль якого дорівнює добутку модуля однієї з сил пари на її плече і який спрямований перпендикулярно площині дії сил пари в ту сторону, звідки пара видно прагне повернути тіло проти годинникової стрілки.
Теорема про суму моментів пари сил. Сума моментів сил, що входять до складу пари, щодо будь-якої точки не залежить від вибору цієї точки і дорівнює моменту цієї пари сил.
Доказ: Виберемо довільно точку О. Проведемо з неї в точки А і В радіус-вектори (Дивись Рис. 4.2).
Що й потрібно було довести.
Дві пари сил називаються еквівалентними. якщо їх дія на тверде тіло однаково при інших рівних умовах.
Теорема про еквівалентність пар сил. Пару сил, що діє на тверде тіло, можна замінити іншою парою сил, розташованої в тій же площині дії і має однаковий з першою парою момент.
Доказ: Нехай на тверде тіло діє пара сил.
П








Тому еквівалентна системі, а ця система еквівалентна системі, так як еквівалентна нулю.
Таким чином ми задану пару сил замінили іншою парою сил. Доведемо, що моменти у цих пар сил однакові.
Момент вихідної пари сил чисельно дорівнює площі паралелограма, а момент пари сил чисельно дорівнює площі паралелограма. Але площі цих паралелограмів рівні, так як площа трикутника дорівнює площі трикутника.
Що й потрібно було довести.
висновки:
Пару сил як жорстку фігуру можна як завгодно повертати і переносити в її площині дії.
У пари сил можна змінювати плече і сили, зберігаючи при цьому момент пари і площину дії.
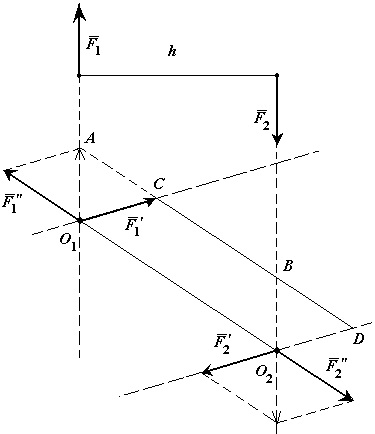
Теорема про перенесення пари сил в паралельну площину. Дія пари сил на тверде тіло не зміниться від перенесення цієї пари в паралельну площину.
Доказ: Нехай на тверде тіло діє пара сил в площині. З точок докладання зусиль А і В опустимо перпендикуляри на площину і в точках їх перетину з площиною докладемо дві системи сил і, кожна з яких еквівалентна нулю.
З
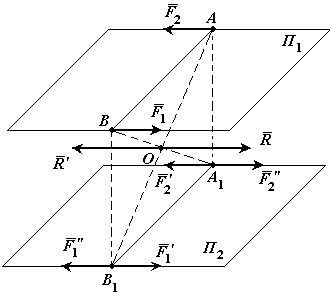



Складемо дві рівні і паралельні сили і. Їх рівнодіюча паралель-на цих сил, дорівнює їх сумі і прикладена посередині відрізка в точці О.
Так як, то система сил еквівалентна нулю і її можна відкинути.
Таким чином пара сил еквівалентна парі сил, але лежить в іншій, паралельній площині. Що й потрібно було довести.
Слідство: Момент пари сил, що діє на тверде тіло, є вільний вектор.
Дві пари сил, що діють на один і той же тверде тіло, еквівалентні, якщо вони мають однакові по модулю і напрямку моменти.
Теорема про складання пар сил. Дві пари сил, що діють на один і той же тверде тіло, і що лежать в пересічних площинах, можна замінити однією еквівалентної парою сил, момент якої дорівнює сумі моментів заданих пар сил.
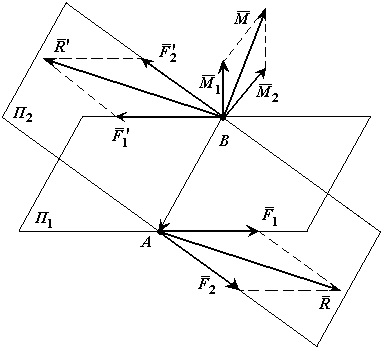
Доказ: Нехай є дві пари сил, розташовані в пересічних площинах. Пара сил в площині характеризується моментом, а пара сил в площині характеризується моментом.
Розташуємо пари сил так, щоб плече пар було загальним і розташовувалося на лінії перетину площин. Складаємо сили, прикладені в точці А і в точці В,. Отримуємо пару сил.
Що й потрібно було довести.
^
Умови рівноваги пар сил.
Якщо на тверде тіло діє кілька пар сил, як завгодно розташованих в просторі, то послідовно застосовуючи правило паралелограма до кожним двом моментам пар сил, можна скільки завгодно пар сил замінити однією еквівалентної парою сил, момент якої дорівнює сумі моментів заданих пар сил.
Теорема. Для рівноваги пар сил, прикладених до твердого тіла, необ-обхідно і достатньо, щоб момент еквівалентної пари сил дорівнював нулю.
Теорема. Для рівноваги пар сил, прикладених до твердого тіла, необхідно і достатньо, щоб алгебраїчна сума проекцій моментів пар сил на кожну з трьох координатних осей дорівнювала нулю.