У цьому розділі розглянемо формулу, яка б пов'язала подвійний і криволінійний інтеграли.
. інтеграл називається інтегралом по замкнутому контуру.
Домовимося називати позитивним напрямком обходу простого замкнутого контуру то, при якому найближча до спостерігача частина області, обмеженою контуром, виявляється лежить зліва від спостерігача.
Нехай і. т.е.непреривни на (D) і Г- замкнутий кусочногладкій контур, тоді має місце формула:
,яка називається формулою Гріна.
Для виведення формули будемо зводити обчислення інтеграла по замкнутій кривій до інтеграла від області, укладеної всередині цієї кривої.
Розіб'ємо висновок на кілька пунктів:
1) Область D є криволінійна трапеція:
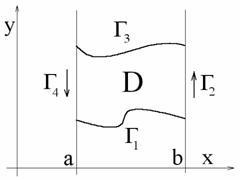
Запишемо тепер інтеграл по контуру у вигляді. а подвійний інтеграл буде виглядати відповідно:
- перша частина рівності доведена.
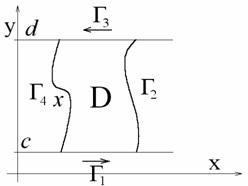
Запишемо тепер інтеграли від окремих ділянок кривої, причому інтеграли від Г2 і Г4 дорівнюватимуть нулю:
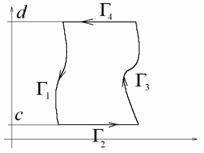
Запишемо подвійний інтеграл у вигляді
. отже, ми довели, що. але раніше ми також довели, що. отже, можна уявити як.
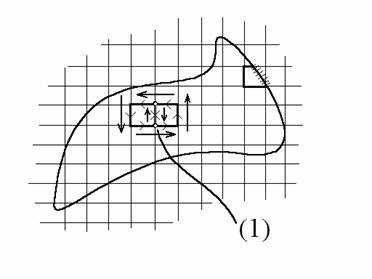
Інтеграл по межі двох елементів (1) дорівнює нулю, так як він обчислюється двічі в протилежних напрямках, отже, сума всіх криволінійних інтегралів буде дорівнює інтегралу по кордоні D.
Розглянемо тепер деякі наслідки з формули Гріна.
Умови незалежності криволінійного інтеграла
від шляху інтегрування в однозв'язної
області на площині
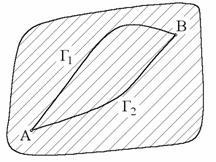
Наступні чотири умови - є умовами еквівалентності:
1) (криві Г1 і Г2 мають однакове початок - точку А і однаковий кінець - точку В)
2) справедливо для будь-якої кусочногладкой замкнутої кривої Г.