Визначення. Лінія, що має в системі координат хоу рівняння виду
Ax 2 + Bxy + Cy 2 + Dx + Ey + F = 0,
де А 2 + В 2 + С 0, називається лінією другого порядку.
До основних лініях другого порядку відносяться: еліпс, коло, гіпербола, парабола. До не основним лініях другого порядку відносяться: пара паралельних або злилися прямих, пара пересічних прямих і крапка.
Определеніе.Елліпсом називається безліч точок площині, сума відстаней від кожної з яких до двох фіксованих точок (фокусів) цієї площини - постійна величина, причому, велика ніж відстань між фокусами.
Якщо фокуси F1. F2 знаходяться на осі ох, а початок координат ділить фокусна відстань F1 F2 навпіл, то еліпс має рівняння
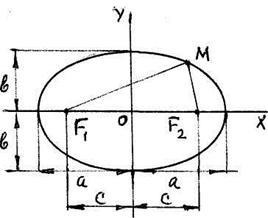
яке виходить шляхом спрощення рівності. якщо врахувати, що відстань (c). мала піввісь (b) і велика піввісь (a) еліпса пов'язані співвідношенням: a 2 = b 2 + c 2.
Определеніе.Окружностью називається безліч всіх точок площині, кожна з яких знаходиться на відстані R від фіксованої точки С цій площині.
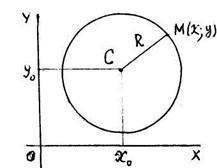
Окружність можна розглядати як граничний випадок еліпса, у якого фокуси поєдналися в одній точці.
Определеніе.Гіперболой називається безліч всіх точок площині, абсолютна величина різниці відстаней від кожної з яких до двох фіксованих точок (фокусів) цієї площини - постійна величина, причому менша ніж відстань між фокусами.
Якщо фокуси F1. F2 знаходяться на осі ох і початок координат ділить фокусна відстань F1 F2 навпіл, то гіпербола має рівняння. яке виходить
шляхо
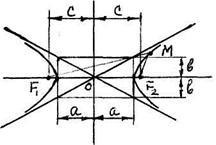
якщо врахувати, що полуфокусное відстань (с). речова піввісь (а). уявна піввісь (в) пов'язані співвідношенням c 2 = a 2 + b 2.
Определеніе.Параболой називається безліч всіх точок площині, кожна з яких однаково віддалена від деякої фіксованої точки (фокуса) і від деякої фіксованої прямої (директриси) цієї площини.
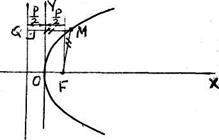
де р - відстань між фокусом і директоркою.
Примітка. Якщо в рівнянні другого ступеня є твір координат (коефіцієнт В 0), то лінія другого порядку повернута на деякий кут щодо осей координат. Наприклад, рівняння ху = 1 визначає гіперболу з параметрами а = b =, повернену щодо осей координат на 45 °. Якщо коефіцієнт У в рівнянні другого ступеня дорівнює 0, то питання про вид та розташуванні лінії легко вирішується виділенням повних квадратів по змінним х і y.
Приклад. Побудувати лінію, задану рівнянням х 2 + 4у 2 - 4х - 8У + 4 = 0 і знайти її параметри.