Сумою а + b двох векторів а і b називається вектор, який йде з початку вектора а в кінець вектора b за умови, що вектор b прикладений до кінця вектора а (правило трикутника) Побудова суми а + b зображено на рис. 42.
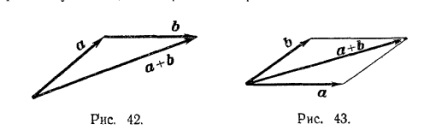
Поряд з правилом трикутника часто користуються (рівносильним йому). правилом паралелограма: якщо вектори а і b приведені до спільного початку і на них побудований паралелограм, то сума а + b є вектор, що збігається з діагоналлю цього паралелограма, що йде із загального початку а й b (рис. 43). Звідси відразу випливає, що a + b = b + а.
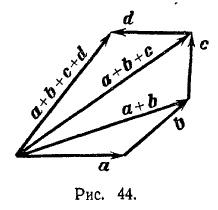
Додавання багатьох векторів проводиться за допомогою послідовного застосування правила трикутника (див. Рис. 44, де зображено побудова суми чотирьох векторів а, b, с, d).
Різницею а - b двох векторів а і b називається вектор, який в сум- а ме з вектором Ь становить вектор а. Якщо два вектори а і b приведені до спільного початку, то різниця їх а - b є вектор, що йде з кінця b ( «від'ємника») до кінця а ( «зменшуваного»). Два вектора рівної довжини, що лежать на одній прямій і спрямовані в протилежні сторони, називаються взаімнообратнимі: якщо один з них позначений символом а, то інший позначається символом -а. Легко бачити, що а - b = а + (- b). Таким чином, побудова різниці рівносильно збільшенню до «зменшуваного» вектора, зворотного «віднімається».
Твором му (або також aα) вектора а на число α називається вектор, модуль якого дорівнює добутку модуля вектора а на модуль числа α; він паралельний вектору а чи лежить з ним на одній прямій і спрямований так само, як вектор а, якщо α - число позитивне, і протилежно вектору а, якщо α - число від'ємне.
Сума векторів та множення вектора на число називаються лінійними операціями над векторами.
Трапляються такі дві основні теореми про проекціях векторів:
1. Проекція суми векторів на якусь вісь дорівнює сумі їх проекцій на цю ж вісь:
2. При множенні вектора на число його проекція множиться «а то ж число:
Зокрема, якщо
Якщо а = (X; Y; Z), то для будь-якого числа α
Вектори, що лежать на одній прямій або на паралельних прямих, називаються колінеарними. Ознакою коллинеарности двох векторів
є пропорційність їх координат:
Трійка векторів i, j, k називається координатним базисом, якщо ці вектори задовольняють таким умовам:
1) вектор i лежить на осі Ох, вектор i - на осі Оу, вектор k - на осі Oz;
2) кожен з векторів i, j, k спрямований на своїй осі в позитивну сторону;
3) вектори i, j, k - одиничні, т. Е. | I | = 1, | j | = 1, | k | = 1
Яким би не був вектор а, він завжди може бути розкладений по базису i, j, k, т. Е. Може бути представлений у вигляді:
коефіцієнти цього розкладання є координатами вектора а (т. е. X, Y, Z суть проекції вектора а на координатні осі).
761. За даними векторах а й b побудувати кожен з наступних векторів: 1) а + b; 2) a - b; 3) b - а; 4) -а - b.
762. Дано: | а | = 13, | b | = 19 і | а + b | = 24. Обчислити | а - b |.
763. Дано: | а | = 11, | b | = 23 і | а - b | = 30. Визначити | а + b |.
764. Вектори а і b взаємно перпендикулярні, причому | а | = 5 і | b | = 12. Визначити | a + b | і | а - b |.
765. Вектори а і b утворюють кут φ = 60 °, причому | а | = 5 і | b | = 8. Визначити | а + b | і | а - b |.
766. Вектори а і b утворюють кут φ = 120 °, причому | а | = 3 і | 6 | = 5. Визначити | a + b | і | а - b |.
767. Якому умові повинні задовольняти вектори а і b, щоб мали місце такі співвідношення: 1) | а + b | = | А - b |; 2) | а + b |> | а-b |; 3) | а + b |