магічні багатогранники

Очевидно, що немає межі комбінаторним задачам, в яких необхідно маркувати ребра, вершини або грані різних багатогранників так, щоб виходили магічні константи, причому найнесподіванішим чином. Багато з цих завдань можуть бути переведені в еквівалентну задачу з магічними зірками. Наприклад, така. Які з п'яти прав

магічні багатогранники
мулових геометричних тіл можна зробити магічними, промаркований їх ребра так, щоб сума чисел в вершинах була однакова? Причому має виконуватися ще одна умова - числа повинні представляти собою послідовний ряд. Легко побачити, що це не тетраедр. Про це ви можете почитати в книзі Sixth Book of Mathematical Games from Scientific American ( «Шоста книга по математичним іграм від журналу Scientific American»). Може бути, це куб? У куба 12 ребер (див. Рисунок ліворуч). Відзначте 12 чорних крапок в вершинах октаграма (праворуч). Оскільки через кожну точку проходять дві лінії, константа повинна дорівнювати (2х78) / 8, або 19,5.

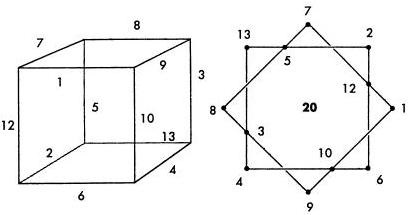
Це число не є цілим, так що тут відповіді шукати не варто. Однак ми можемо отримати неповноцінне рішення (що не задовольняє останньому умові) з найменшою магічною постійної 20 і найменшим максимальним числом 13, промаркований кружечки (і еквівалентні ребра куба), як показано на малюнку.

Оскільки октаедр дуальний кубу, це призводить до автоматичного вирішення завдання щодо маркування ребер октаедра розрізняються непослідовними ненульовими позитивними цілими числами, сума яких навколо кожної грані дає магічну постійну, причому найменшу.

Як ми вже бачили, межі октаедра можна промаркувати послідовними цілими числами таким чином, щоб його вершини стали магічними. Для ікосаедра і Додекаедр магічна постійна виходить дробової, так що вони не можуть бути рішенням завдання. Оскільки все багатогранники мають дуальну пару, то серед них такого, який би задовольняв умовам близькою завдання (цілі, ненульові послідовні числа, але з магічними гранями), не існує.

Матеріали по темі:

Поділитися з друзями:

Контрольні роботи по:

Курсові роботи по:

Схожі статті