Математичне сподівання числа влучень і середній очікуваний витрата боєприпасів і часу
123. Математичним очікуванням числа влучень називається середнє число влучень, яке можна отримати, якщо повторити стрілянину велике число раз в можливо однакових умовах.
Математичне сподівання числа влучень при декількох пострілах (а n), якщо ймовірність попадання (р) для всіх пострілів однакова, дорівнює добутку кількості пострілів (n) на ймовірність попадання при одному пострілі, т. Е.
Для випадку, коли ймовірність попадання від пострілу до пострілу змінюється:
де Р1. Р2. і Рn - ймовірність попадання при відповідному пострілі.
Приклад. Визначити математичне сподівання числа влучень при 5 пострілах з ручного кулемета Калашникова, якщо ймовірність попадання при одному пострілі дорівнює 0,4 і від пострілу до пострілу не змінюється.
Рішення. Математичне сподівання числа влучень одно
Це означає, що при великій кількості стрільб по 5 пострілів иа кожну стрілянину припадатиме в середньому по 2 попадання.
124. Середній очікуваний витрата боєприпасів, необхідних для ураження цілі, дорівнює частці від ділення необхідного числа влучень (математичного очікування числа влучень) на ймовірність попадання при одному пострілі, т. Е.
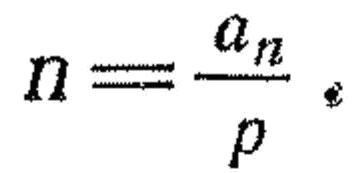
Для стрільби по живих цілях необхідне число влучень дорівнює: при стрільбі одиночними пострілами, коли можливе спостереження за результатами кожного пострілу і стрілянина припиняється відразу ж після ураження цілі, - одному попаданню; при стрільбі автоматичним вогнем - математичного сподівання числа влучень. розрахованому виходячи із заданої ймовірності ураження цілі (надійності стрільби).
Математичне сподівання числа влучень в залежності від заданої ймовірності ураження цілі вказано в табл. 3 додатка 4,
Приклад 1. Визначити середнє очікуване кількість патронів, необхідне для отримання одного влучення при стрільбі з самозарядного карабіна Симонова в спостерігача противника, якщо ймовірність попадання р = 0,20.
Приклад 2. Визначити середнє очікуване кількість патронів, необхідне для ураження групової мети, що складається з втікачів фн-гур иа фронті 20 м на відстані 400 м, при стрільбі з станкового кулемета Горюнова з розсіюванням по фронту, якщо ймовірність попадання в ціль р = 0, 03 і потрібно вразити ціль з надежностьюPi = 0,50, або 50%.
Рішення. 1. З табл. 3 додатка 4 знаходимо, що ймовірності ураження (надійності стрільби) Pi = 0,50 відповідає математичне очікування числа влучень аn = 0,7.
2. Визначаємо середнє очікуване кількість патронів, необхідне для ураження цілі:
Середній очікуваний витрата патронів (гранат) для ураження цілі характеризує економічність стрільби, т, е. Показує, якою кількістю боєприпасів можна в середньому вирішити дану вогневу задачу.
Середній очікуваний витрата патронів для ураження груповий мети при стрільбі з розсіюванням по фронту можна також визначити за формулою
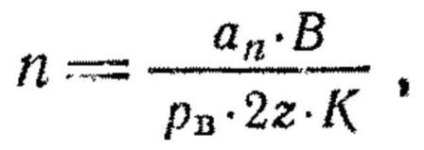
де п - кількість патронів, необхідне для ураження заданого числа (відсотка) фігур;
ап - математичне очікування числа влучень, рівне: для ураження 80% фігур - 1,609; для ураження 50% фігур - 0,693 попадання (в додатку 4, табл. 3 ці величини округлені);
В - ширина фронту в м, зайнятого цілями;
р в - ймовірність попадання в смугу »рівну висоті мети;
2z - ширина окремої мети; / (- т-коефіцієнт фігурного мети.
125. Середній очікуваний витрата патронів (п) для ураження цілі при стрільбі чергами дорівнює числу пострілів в черзі (s), поділеній на ймовірність ураження целн при даній довжині черги (Pi), т. Е.
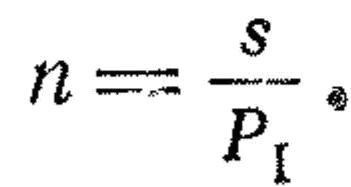
Кількість патронів, дане в таблицях стрільби, розраховане виходячи з характеристики розсіювання для кращих стрільців та довжини черги в 3 патрони.
Приклад. Визначити середню кількість патронів (n), необхідне для ураження кулемета при стрільбі чергами (s) по 3 патрони па відстань 400 м, якщо ймовірність ураження цілі при одній черзі в 3 постріли Pi = 0,54, або 54%.
Рішення. Визначимо середній очікуваний витрата патронів:
Якщо відома ймовірність попадання в ціль (р) і задана надійність стрільби (Pi), то середній очікуваний витрата патронів (п) може бути визначено по табл. 4 додатка 4.
126. Середнє очікуване час на виконання вогневої задачі складається з часу на підготовку стрільби і часу на стрільбу. Час на саму стрілянину визначається діленням середнього очікуваного витрати боєприпасів на бойову скорострільність зброї з урахуванням режиму вогню.
Середнє очікуване час, так само як і середній очікуваний витрата боєприпасів, характеризує економічність стрільби.
Найвигідніші значення надійності і еконоічності стрільби будуть при найбільшої ймовірності попадання