транскрипт
1 Крайова науково-практична конференція навчально-дослідних і проектних робіт учнів 6-11 класів «Прикладні і фундаментальні питання математики» прикладні питання математики Математичне вишивання Треногіна Ангеліна Валеріївна, 10 кл. МАОУ «Ліцей 9» м Пермі, Тарасова Олена Анатоліївна, учитель математики. Перм
3 ВСТУП. «Людині необхідний порядок: без нього все його дії втрачають узгодженість, логічний взаємозв'язок. Чим досконаліша порядок, тим спокійніше і впевненіше почувається людина. Він робить умоглядні побудови, грунтуючись на порядок, який продиктований йому потребами його психіки, - це творчий процес. Творчість є акт впорядкування »Ле Корбюзьє (відомий французький архітектор) Чому я вибрала цю тему? Людина вміє інтуїтивно відчувати гармонію. Його притягує те, що несе в собі гармонію, і відштовхує дисгармонія. Гармонійні структури ми називаємо словом «краса». Назва моєї теми «Математичне вишивання» вже говорить про порядок, який закладений в основу творчого процесу і у мене виникло бажання зануритися в цю область прикладного характеру науки математики. Чим актуальна ця тема? Деякі люди вважають математику нудною і тьмяною, але через цю тему я покажу, наскільки красивою і барвистою може бути математика, як привабливі і різноманітні фігури і що можна побудувати за допомогою начебто звичайної окружності. 3
if ($ this-> show_pages_images $ Page_num doc [ 'images_node_id'])
4 Мета роботи: Показати, що математика як наука виникла з потреб людської практики і розвивалася в ній, тобто: 1. Показати шляхи взаємодії і взаємозбагачення науки і мистецтва 2. Розширити уявлення про сфери застосування математики 3. Показати, що фундаментальні закономірності математики є формотворними в прикладному мистецтві. Етапи роботи: 1. Вивчення теоретичного матеріалу по темі. 2. Практичне застосування отриманих знань. 3. Висновок 4


5 МАТЕМАТИКА І ВИШИВАННЯ? Павутини створюються в природі, їх плете павук, і вони неймовірно красиві, здається, що людина не здатна створити таку красу сам, але ось і ні. За допомогою математичного розрахунку ці криві можна сплести так, що вийде будь-яка, найдосконаліша за своєю красою павутина. ПАВУК ЛЮДИНА В XIX столітті в жіночих школах був введений предмет «Математичне вишивання». На заняттях вивчався спосіб побудови кривих, який називався методом математичного вишивання. Крім його привабливості, рішення задач способом математичного вишивання дозволяє розширити геометричні уявлення, розвиває акуратність, уважність і працьовитість. Так як математичне вишивання грунтується на побудові кривих, нам неодмінно потрібно познайомитися з цим поняттям. 5




6 ЧУДОВІ КРИВІ Поняття кривої не отримує виразною формулювання і іноді визначається як «довжина без ширини» або як «межа фігури». Але криві ми можемо помітити і в природі, і в оточуючих нас предметах. Наприклад, в траєкторії кинутого каменя, обрис квітки і пелюстках рослин, звивиста лінія берега річки і інші явища з давніх пір зацікавили людей. Спостережувані багаторазово вони послужили основою для поступового встановлення поняття лінії. Вивченням кривих займалися багато механіки, астрономи, математики. З численних видів кривих можна виділити групу ліній, які нагадують нам форми квітів, листя клена, щавлю, верби і т.д. цю групу вирішили називати циклоїдальні криві. Вони мають величезне 6
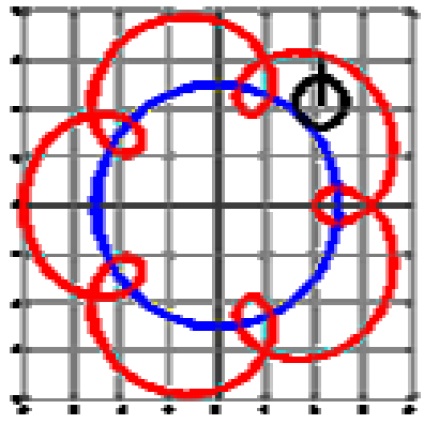

7 значення для техніки. Обрис багатьох видів акцентіровок та інших деталей машин мають вигляд саме цих кривих. Циклоїдальних кривої називають траєкторію точки, постійно пов'язаної з колом котиться без ковзання по іншій окружності. (Малюнки) Чим же пояснюється таке різноманіття кривих? По-перше, це залежить від розташування викреслюють точки: вона може перебувати на котиться кола або на деякій відстані від неї. По-друге, окружності можуть кататися з внутрішньої і з зовнішнього боку. Якщо окружності котиться по іншій окружності з внутрішньої сторони, то циклоїдні криві називають гіпоціклаіднимі. Якщо ж вона котиться по зовнішній стороні, то її називають епіціклоідние. Кардіоїда (Cardioid) Кардіоїда вперше зустрічається в працях французького вченого Луї Карре. Назва кривої, дав Джованні Кастильони. Надалі до кривої проявляли інтерес багато видних математики XVIII-XIX століть. Якщо використовувати дві окружності з однаковими радіусами і обертати одну навколо іншої, то вийде кардіоїда (греч.кардіа - серце) - на думку математиків, одержувана крива віддалено нагадує серце. Равлик Паскаля Лімакона або Равлик Паскаля була відкрита французьким математиком Етьєном Паскалем (батьком знаменитого вченого Блеза Паскаля) 7
8 Якщо взяти точку не на самій котиться кола, а всередині її, змістивши в бік від центру? Тоді ми отримаємо криву, отриману назву Равлик Паскаля. Спіраль Архімеда спіраль Архімеда - плоска крива, яку описує точка, що рухається рівномірно поступально від центру 0 по равномерновращающемуся радіусу. 8
9 МОЇ РОБОТИ Я теж вирішила спробувати позайматися Математичним вишиванням і вишила кілька кривих. Нефроіда Алгоритм вишивання: На колі з картону я провела, окружність меншого радіуса і зазначила, на ній точку А. Почавши з точки А, розділила окружність на дуги по 10 0 і пронумеровані точки поділу числами 1, 2, 3 (номер 1 відповідає точці А ). А потім за допомогою голки з ниткою поєднала числа 1 і 3, 2 і 6, 3 і 9, (т. Е точки з номерами n і 3n). В результаті вийшла крива Нефроіда. кардіоїда 9
10 Алгоритм вишивання: Так само на колі з картону я провела коло з діаметром АВ. Почавши з точки А, розділила окружність на дуги по 10 0 (точці А відповідає число 0). Потім, почавши з точки В, розбила окружність, в тому ж напрямку, на дуги вже по 20 0 і пронумеровані точки іншим кольором (точці В відповідає число 0). І за допомогою голки з ниткою поєднала однакові номери. В результаті отримало криву кардіоїда. дельтоида 10
11 Алгоритм вишивання: На колі з картону я провела коло і розділила її на три рівних кута з вершиною збігається з центром кола, а потім використовувала техніку математичного вишивання заповнення кута, тобто кожну сторону кута розбила на рівні відрізки (кількість відрізків на сторонах кута має дорівнювати) і пронумеровані кожну сторону в різних напрямках, а потім з'єднала однакові числа. Так я заповнила всі три кути і отримала дельтоидов. 11
12 Астроіда Алгоритм вишивання: Для того що б вишити астроїда я використовувала той же метод, що і в дельтоидов, тільки окружність я розділила на чотири кути і так же заповнила їх методом заповнення кута. 12
13 ВИСНОВОК: Тема мені сподобалася відразу і в результаті її вивчення, я зрозуміла універсальність математичних знань і законів в навколишньому світі. Матеріал було знайти досить важко, але я впевнена, що все знання, які я отримала в ході підготовки, знадобляться мені і в майбутньому. Вивчення теми «Математичне вишивання» дозволило мені розширити геометричні уявлення, розвинути акуратність, уважність і працьовитість. Я отримала велике задоволення від процесу вишивання математичних кривих і результатів своєї роботи. Математика вражає своєю красою і багатством змісту. Вона так багатогранна і місцями можливо навіть не зрозуміла Є ще стільки цікавого в математиці, чого ми не знаємо, то, що нам ще належить зрозуміти. Але поки нам слід користуватися тим, що відкрили для нас знамениті математики. 13
14 ЛІТЕРАТУРА: 1. Савелов А. А. Плоскі криві: Либроком 1960 р с. 2. Математичний енциклопедичний словник: Радянська енциклопедія, 1988 р с. 14