ВИДИ КОМП'ЮТЕРНОЇ ГРАФІКИ
Комп'ютерна графіка - область інформатики, що вивчає методи і засоби створення та обробки зображень за допомогою програмно-апаратних обчислювальних комплексів. Комп'ютерна графіка є однією з найбільш бурхливо розвиваються галузей інформатики та в багатьох випадках виступає «локомотивом», який тягне за собою всю комп'ютерну індустрію.
Області застосування КГ:
- медицина (комп'ютерна томографія);
- наукові дослідження (візуалізація будови речовини, векторних полів і інших даних);
- моделювання тканин та одягу;
- дослідно-конструкторські розробки, І.Д.
Залежно від способу формування зображень КГ ділиться на: растрову, векторну, фрактальную і 3D.
Для растрових зображень, що складаються з точок, особливу важливість має поняття дозволу, що виражає кількість точок, що припадають на одиницю довжини. При цьому слід розрізняти:
• дозвіл екранного зображення;
• дозвіл друкованого зображення.
Дозвіл оригіналу. Дозвіл оригіналу вимірюється в точках на дюйм (dotsper inch - dpi) і залежить від вимог до якості зображення і розміру файлу, способу оцифрування або методу створення початкової ілюстрації, вибраного формату файлу та іншим параметрам. У загальному випадку діє правило: чим вище вимоги до якості, тим більша має бути дозвіл оригіналу.
Дозвіл екранного зображення. Для екранних копій зображення елементарну точку растра прийнято називати пикселом. Розмір пікселя варіюється в залежності від обраного екранного дозволу (з діапазону стандартних значень), дозволу оригіналу і масштаб.
Монітори для обробки зображень з діагоналлю 20-21 дюйм (професійного класу), як правило, забезпечують стандартні екранні дозволи 640x480, 800x600, 1024x768, 1280x1024, 1600x1200, 1600x1280, 1920x1200, 1920x1600 точок. Відстань між сусідніми точками люмінофора у якісного монітора складає 0,22-0,25 мм.
Дозвіл друкованого зображення і поняття лініатури. Розмір точки растрового зображення як на твердій копії (папір, плівка і т. Д.), Так і на екрані залежить від застосованого методу та параметрів растрування оригіналу. При раструванні на оригінал як би накладається сітка ліній, комірки якої утворюють елемент растра. Частота сітки растра вимірюється числом ліній на дюйм і називається линиатурой.
Масштабування растрових зображень. Одним з недоліків растрової графіки є так звана пикселизация зображень при їх збільшенні (якщо не прийняті спеціальні заходи). Раз в оригіналі присутня певна кількість точок, то при більшому масштабі збільшується і їх розмір, стають помітні елементи растру, що спотворює саму ілюстрацію (рис. 1). Для протидії пикселизации прийнято заздалегідь оцифровувати оригінал з дозволом, достатнім для якісної візуалізації при масштабуванні.
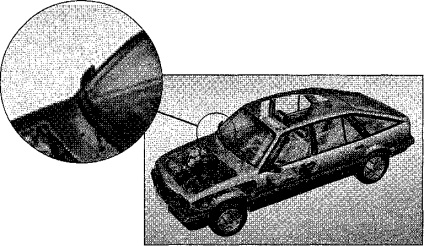
Мал. 1. Ефект пикселизации при масштабуванні растрового зображення
Якщо в растровій графіці базовим елементом зображення є точка, то у векторній графіці - лінія. Лінія описується математично як єдиний об'єкт, і тому об'єм даних для відображення об'єкта засобами векторної графіки істотно менше, ніж в растровій графіці.
Лінія - елементарний об'єкт векторної графіки. Як і будь-який об'єкт, лінія володіє властивостями: формою (пряма, крива), товщиною, кольором, шрифтом (суцільна, пунктирна). Замкнені лінії набувають властивість заповнення. Охоплюється ними простір може бути заповнений іншими об'єктами або вибраним кольором.
Найпростіша незамкнута лінія обмежена двома точками, які називали вузлами. Вузли також мають властивості, параметри яких впливають на форму кінця лінії і характер сполучення з іншими об'єктами.
Всі інші об'єкти векторної графіки складаються з ліній. Наприклад куб можна скласти з шести пов'язаних прямокутників, кожен з яких, в свою чергу, утворений чотирма зв'язаними лініями. Можливо уявити куб і як дванадцять пов'язаних ліній, що утворюють ребра.
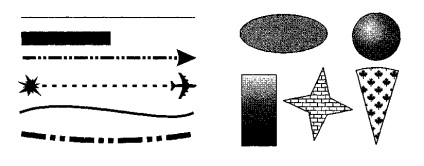
Мал. 2. Об'єкти векторної графіки
Математичні основи векторної графіки
Розглянемо докладніше способи представлення різних об'єктів в векторної графіки.
Крапка. Цей об'єкт на площині представляється двома числами (х, у), що вказують його положення щодо початку координат.
Пряма лінія. Їй відповідає рівняння у = kx + b. Вказавши параметри k і Ь, завжди можна відобразити нескінченну пряму лінію у відомій системі координат, тобто для завдання прямої достатньо двох параметрів.
Відрізок прямої. Він відрізняється тим, що вимагає для опису ще двох параметрів - наприклад, координат xl і х2 початку і кінця відрізка.
Крива другого порядку. До цього класу кривих відносяться параболи, гіперболи, еліпси, кола, тобто всі лінії, рівняння яких містять ступені не вище другої. Крива другого порядку не має точок перегину. Прямі лінії є всього лише окремим випадком кривих другого порядку. Формула кривої другого порядку в загальному вигляді може виглядати, наприклад, так:
Таким чином, для опису нескінченної кривої другого порядку досить п'яти параметрів. Якщо потрібно побудувати відрізок кривої, знадобляться ще два параметри.
Крива третього порядку. Відмінність цих кривих від кривих другого порядку полягає в можливу наявність точки перегину. Наприклад графік функції у = х? має точку перегину на початку координат (рис. 15.5). Саме ця особливість дозволяє зробити криві третього порядку основою відображення природних об'єктів у векторній графіці. Наприклад лінії вигину людського тіла вельми близькі до кривим третього порядку. Всі криві другого порядку, як і прямі, є окремими випадками кривих третього порядку.
У загальному випадку рівняння кривої третього порядку можна записати так:
Таким чином, крива третього порядку описується дев'ятьма параметрами. Опис її відрізка зажадає на два параметри більше.
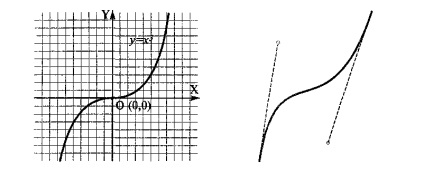
Мал. 3. Крива третього порядку (зліва) і крива Безьє (праворуч)
Криві Безьє. Це особливий, спрощений вигляд кривих третього порядку. Метод побудови кривої Безьє (Bezier) заснований на використанні пари дотичних, проведених до відрізка лінії в її закінченнях. Відрізки кривих Безьє описуються вісьмома параметрами, тому працювати з ними зручніше. На форму лінії впливає кут нахилу дотичної та довжина її відрізка. Таким чином, дотичні відіграють роль віртуальних "важелів", за допомогою яких керують кривої.