Матрична алгебра - Трикутні матриці
Квадратна матриця називається трикутною. якщо її елементи, що стоять вище (нижче) головної діагоналі, дорівнюють нулю. Наприклад, матриця
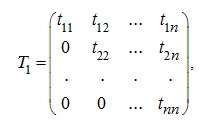
де є верхньою треугольнойматріцей. а матриця

де є нижньою трикутною матрицею.
Діагональна матриця є окремим випадком трикутної матриці (як верхній, так і нижній). Очевидно, що визначник трикутної матриці дорівнює добутку її діагональних елементів. тобто в наших прикладах:
Тому трикутна матриця є невироджених тоді і тільки тоді, коли всі її діагональні елементи відмінні від нуля.
Сума і твір трикутних матриць однієї і тієї ж розмірності і однаковою структури (тобто, обидві - верхні, або обидві - нижні) є також трикутними матрицями тієї ж розмірності і структури.
Зворотній матриця невироджених трикутної матриці - також трикутна матриця тієї ж розмірності і структури. Виходячи з цього, звернення трикутної матриці не викликає ніяких труднощів.