Загальний вигляд нелінійного рівняння:
де функція f (x) визначена і неперервна на кінцевому або нескінченному інтервалі [a, b].
Будь-яке число, що звертає функцію f (x) в нуль, називається коренем рівняння (1). Нелінійні рівняння поділяються на алгебраичен-ські і трансцендентні.
Рівняння (1) називається алгебраїчним, якщо функція f (x) є алгебраїчною. Рівняння (1) називається трансцендентним, якщо функція f (x) не є алгебраїчною.
Вирішити рівняння (1) означає наступне:
1) встановити, чи має рівняння коріння.
2) визначити кількість коренів.
3) знайти значення коренів із заданою точністю.
Перші два етапи називають відділенням коренів. Відділення коренів - процедура знаходження відрізків, на яких рівняння (1) має тільки один корінь. У більшості випадків відділення коренів можна провести графічно. Для цього досить побудувати графік функції F (x) і визначити відрізки, на яких функція F (x) має тільки одну точку перетину з віссю абсцис (інтервали ізоляції).
Після визначення інтервалів ізоляції вдаються до різних методів уточнення коренів ..
Методи уточнення кореня
Вважаємо, що відділення коренів рівняння (1) проведено і на відрізку ізоляції [а, b] розташований один корінь, який необхідно уточнити з похибкою-ністю e (рис. 1).
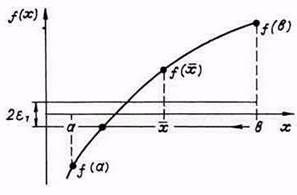
Малюнок 2. Метод дихотомії
Метод дихотомії, або половинного ділення, полягає в наступному. Визначаємо середину відрізка [а, b]. і обчислюємо функцію. Далі робимо вибір, яку з двох частин відрізка взяти для подальшого уточнення кореня. Якщо ліва частина рівняння f (x) є безперервна функція аргументу х. то корінь буде знаходитися в тій половині відрізка, на кінцях якої f (x) має різні знаки. На рис. 3 це буде відрізок [а,], тобто для чергового кроку уточнення точку b переміщаємо в середину відрізка і продовжуємо процес ділення як з початковим відрізком [а, b].
Ітераційний (повторюваний) процес будемо продовжувати до тих пір, поки інтервал [а, b] не стане менше заданої похибки e:
або коли значення функції f (x) (невязка) не стануть досить малі