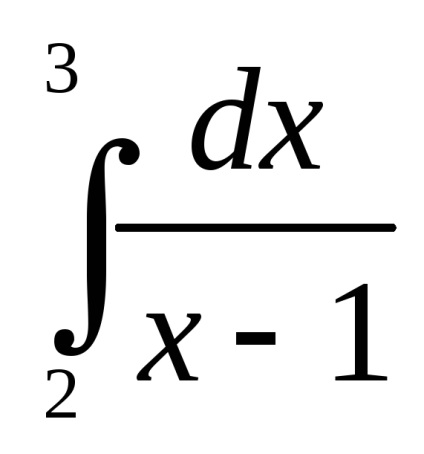метод хорд

Для обчислення визначеного інтеграла

метод хорд
використовують квадратурні формули виду

метод хорд

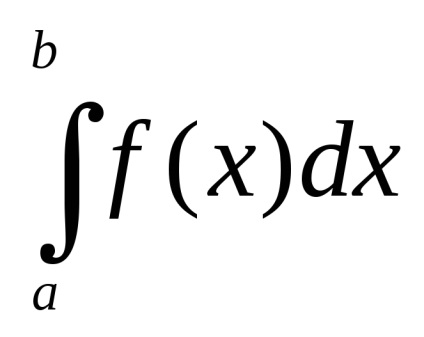
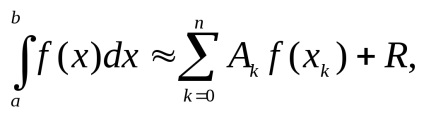
де xk і Ak визначаються квадратурной формулою, R - залишковий член або похибка квадратурної формули.

Відрізок інтегрування [a, b] розбивається на n рівних частин системою рівновіддалених точок xi = x0 + ih. де i = 0,1,2. n; x0 = a, xn = b.

метод хорд
- крок розбиття. Потім обчислюємо підінтегральної функції в отриманих вузлах: yi = f (xi).

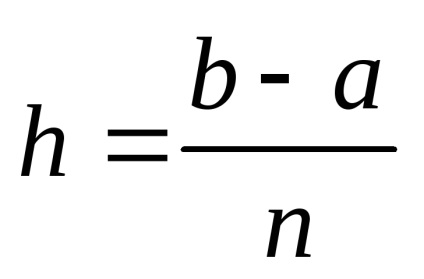
Квадратурні формули для рівновіддалених вузлів:

1) формула лівих прямокутників:

де yi = f (xi), xi = a + ih;

2) формула правих прямокутників:

де yi = f (xi), xi = a + ih;

3) формула центральних прямокутників:

де yi = f (xi),

метод хорд

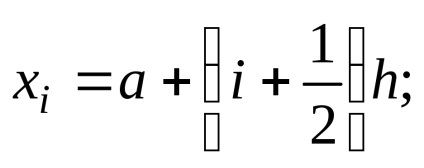
4) формула трапецій:

де yi = f (xi), xi = a + ih;

5) формула Сімпсона (формула парабол):

де yi = f (xi), xi = a + ih.

метод хорд

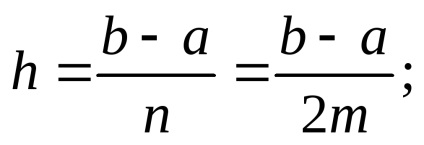
6) формула Ньютона (правило

метод хорд
):

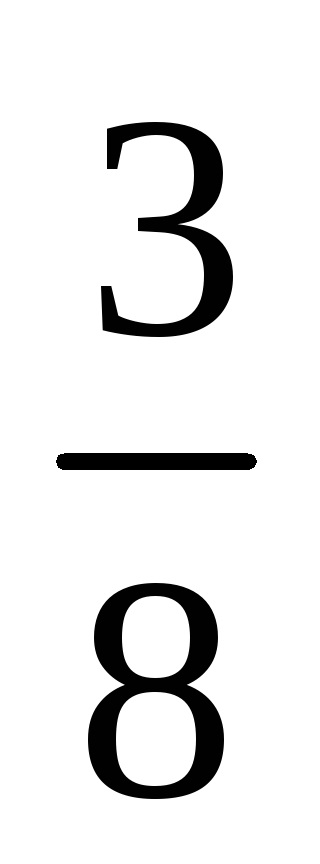
де yi = f (xi), xi = a + ih.

метод хорд
.

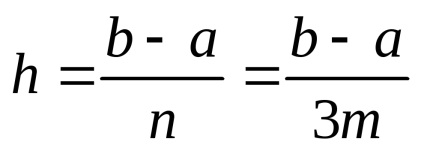
Інтеграли вважаються за допомогою квадратурних формул з точністю . Для того, щоб досягти необхідної точності обчислення . використовується спосіб подвійного перерахунку. інтеграл обчислюють за обраною квадратурній формулі двічі, спочатку з деяким кроком h. потім з кроком

метод хорд
, тобто подвоюють чіслоn (кількість точок розбиття [a, b]).

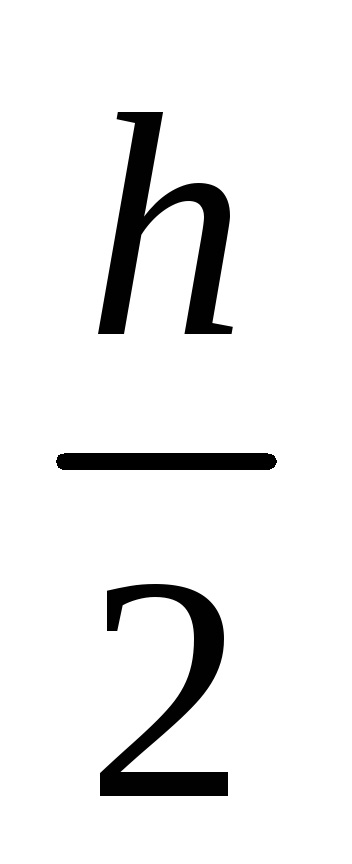
Позначимо результати розбиття через Jn і J2n відповідно і порівняємо їх. Якщо | Jn-J2n |<. где  – погрешность вычислений, то в качестве результата берут J2n . Если |Jn-J2n|. то вычисления повторяют с шагом

метод хорд
і т.д.

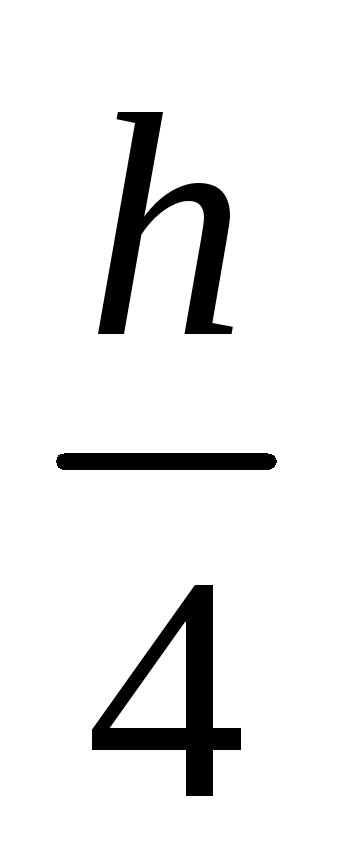
Приклад. За допомогою формули трапецій обчислити інтеграл

метод хорд
з точністю  = 0.01.

Схожі статті