ВСТУП.
Описаний метод використовується в програмі "Просте формування маршрутів. Робота з картою. Розрахунок оптимальних варіантів доставки"
У статті "Оптимізація планування доставки вантажів. Алгоритм кластеризації k-means (метод K-середніх)" було показано, ЯК ОТРИМАТИ ОПТИМАЛЬНІ МАРШРУТИ ДЛЯ ЗАДАНОГО КІЛЬКОСТІ А / ТРАНСПОРТУ із зазначеного місця відвантаження, при цьому вантажопідйомність транспорту не бралася до уваги.
У цій статті покажемо ЯК ДІЗНАТИСЯ КІЛЬКІСТЬ НЕОБХІДНОГО А / ТРАНСПОРТУ З УРАХУВАННЯМ ЙОГО ВАНТАЖОПІДЙОМНОСТІ ДЛЯ ФОРМУВАННЯ ОПТИМАЛЬНИХ МАРШРУТІВ.
Отже, поставлена задача відшукати найвигідніший маршрут руху транспорту, що проходить по одному разу через зазначені пункти з подальшим поверненням в початковий пункт (база). Критеріями оптимальності в даній постановці завдання є: мінімальний пробіг транспортного засобу при максимальному завантаженні кузова.
Сформульована задача відома як «завдання комівояжера». Існує безліч математичних методів, що дозволяють знайти як точне, так і наближене рішення поставленої задачі. Серед методів, що дають точне рішення, найбільш відомі:
Основним недоліком даних методів є висока тимчасова і емкостная складність, що важливо враховувати при великій кількості пунктів. Всі ефективні (скорочують повний перебір) методи вирішення «завдання комівояжера» - методи евристичні. З них найбільше застосування знайшли:
- «Метод генетичних алгоритмів»
- «Метод Кларка-Райта»
- «Алгоритм мурашиної колонії»
- «Метод найближчого сусіда»
- «Метод включення найближчого міста»
- «Метод найдешевшого включення»
Для вирішення нашої задачі найбільш прийнятним методом є метод Кларка-Райта. Він відноситься до числа наближених, ітераційних методів і може використовуватися для комп'ютерного розв'язання задачі розвезення. Похибка рішення не перевищує в середньому 5-10%. Перевагами методу є його простота, надійність і гнучкість, що дозволяє враховувати цілий ряд додаткових факторів, що впливають на кінцеве рішення задачі.
Розглянемо на прикладі, як застосовувати метод Кларка-Райта.
ПОСТАНОВКА ЗАДАЧІ.
З вихідного пункту, в якому розташовується вантажний термінал (склад), необхідно доставити вантажі 12 одержувачам.
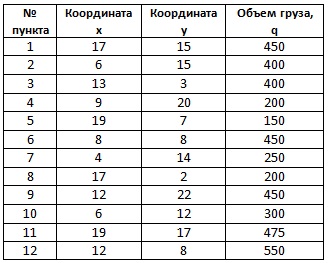
Таблиця 1. Координати і обсяг попиту одержувачів
Координати вантажного терміналу (складу): x0 = 10, y0 = 15. Для доставки буде використовуватися транспорт з максимальною г рузовместімостью = 1500 шт.
ПИТАННЯ: Яка кількість транспорту знадобиться для розвезення вантажів. Яка схема розвезення буде оптимальною?
ПІДГОТОВЧА РОБОТА.
Відзначимо ці точки в декартовій системі координат. Місцезнаходження оптової бази і 12 одержувачів, а також обсяг поставок кожному одержувачу наведені на малюнку 1.
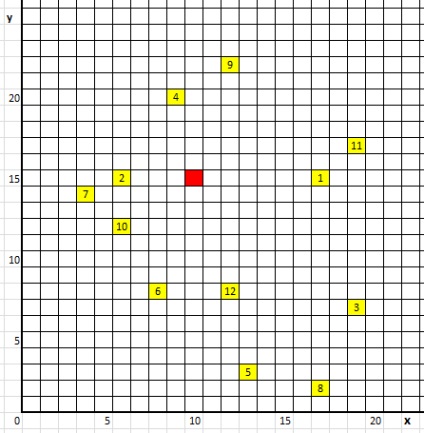
Малюнок 1. Розташування бази і пунктів доставки
Початкова схема маршрутів передбачає що для доставки вантажу кожного окремого одержувачу організовується окремий маршрут (див. Рис. 2). Наприклад, водій завантажує в кузов партію 450 шт. і везе її в пункт 1, там розвантажується, потім повертається на базу, бере другу партію 400 шт. і везе її в пункт 2 і т.д. Таким чином, вихідна схема розвезення включає в себе тільки радіальні маршрути руху автомобіля, причому кількість радіальних маршрутів збігається з кількістю одержувачів. В даному випадку, схема розвезення складається з 12 радіальних маршрутів.
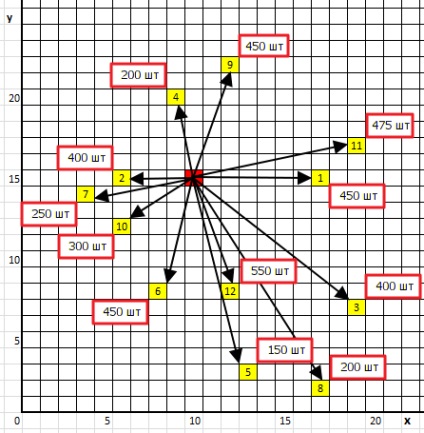
Малюнок 2. Початкова схема доставки вантажу
Суть методу полягає в тому, щоб, відштовхуючись від вихідної схеми розвезення, по кроках перейти до оптимальної схемою розвезення з кільцевими маршрутами. З цією метою вводиться таке поняття, як кілометровий виграш.
На малюнку 3. відображені дві схеми доставки. Схема доставки А (зліва) забезпечує доставку вантажів в пункти 1 і 2 по радіальних маршрутах. В цьому випадку сумарний пробіг автотранспорту дорівнює:
La = d01 + d10 + d02 + d20 = 2d01 + 2d02
Схема доставки B передбачає доставку вантажів в пункти 1 і 2 по кільцевому маршруту. Тоді пробіг автотранспорту становить:
Схема В за показником пробігу автотранспорту дає, як правило, кращий результат, ніж схема А. І тому при переході від схеми А до схеми В отримуємо наступний кілометровий виграш:
S12 = La - L в = d01 + d02 - d12
У загальному випадку ми маємо кілометровий виграш:
де Sij - кілометровий виграш, одержуваний при об'єднанні пунктів i і j, км; d0i, d0j - відстань між оптовою базою і пунктами i та j відповідно, км; dij - відстань між пунктами i та j, км.
Отримані значення заносяться в таблицю 2. де представлені відстані між пунктами dij (права верхня частина матриці) і кілометрові виграші Sij (ліва нижня частина матриці).
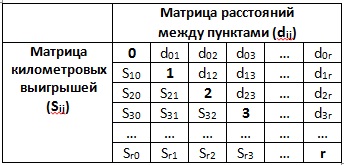
Таблиця 2. Матриця відстаней і кілометрових виграшів
Тепер повернемося до нашого прикладу. З табл. 1 візьмемо дані:
- Пункт 0 (це база): x0 = 10, y0 = 15
- Пункт 1: х1 = 17, у1 = 15
- Пункт 2: х2 = 6, у2 = 15
- Пункт 3: x3 = 13, y3 = 3
- і т.д.
Розрахуємо відстань d01 між пунктами 0 і 1 по формулі:
Аналогічно отримуємо відстань:
- для пунктів 0 і 2. d02 = 4
- для пунктів 0 і 3. d03 = 12,37
- для пунктів 1 і 2. d12 = 11
- для пунктів 1 і 3. d13 = 12,65
- для пунктів 2 і 3. d23 = 13,89
- і т.д
Потім для пунктів i і j отримуємо кілометровий виграш Sij = d0i + d0j - dij.
- для пунктів 1 і 2. S12 = d01 + d02 - d12 = 7 + 4 - 11 = 0
- для пунктів 1 і 3. S13 = d01 + d03 - d13 = 7 + 12.37 - 12.65 = 6.72
- для пунктів 2 і 3. S13 = d02 + d03 - d23 = 4 + 12.37 - 13.89 = 2.48
- і т.д.
Отримані значення заносимо в таблицю 3 .. де представлені відстані між пунктами dij (права верхня частина матриці) і кілометрові виграші sij (ліва нижня частина матриці):
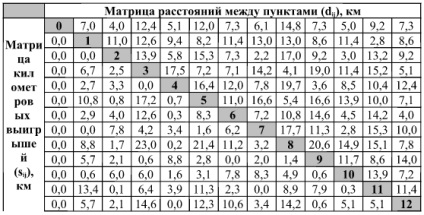
Таблиця 3. Розрахункова м атріца відстаней і кілометрових виграшів
Тепер, коли проведена вся необхідна підготовча робота, приступимо безпосередньо до вирішення завдання.
Покроковий опис алгоритму КЛАРКА-РАЙТА.
На матриці кілометрових виграшів знаходимо осередок (i *, j *) з максимальним кілометровим виграшем Smax:
При цьому повинні дотримуватися наступні три умови:
- пункти i * і j * не входять до складу одного і того ж маршруту;
- пункти i * і j * є початковим і / або кінцевим пунктом тих маршрутів, до складу яких вони входять;
- осередок (i *, j *) чи не заблокована (тобто розглядалася на попередніх кроках алгоритму).
Якщо вдалося знайти такий осередок, яка задовольняє трьом зазначеним умовам, то перехід до кроку 2. Якщо не вдалося, то перехід до кроку 6.
Маршрут, до складу якого входить пункт i *, позначимо як маршрут 1. Відповідно, маршрут, до складу якого входить пункт j *, позначимо як маршрут 2.
Введемо такі умовні позначення:
N = - безліч одержувачів;
- підмножина пунктів, що входять до складу маршруту 1;
- підмножина пунктів, що входять до складу маршруту 2.
Очевидно, що (відповідно до кроку 1, умова 1).
Розрахуємо сумарний обсяг поставок за маршрутами 1 і 2:
де qk - обсяг попиту k-го пункту, шт (див табл. 4).
Перевіримо на виконання таких умов:
де c - вантажомісткість автомобіля, шт.
Якщо умова виконується, то перехід до кроку 4. якщо немає - до кроку 5.
Виробляємо об'єднання маршрутів 1 і 2 в один загальний кільцевий маршрут X. Будемо вважати, що пункт i * є кінцевим пунктом маршруту 1, а пункт j * - початковим пунктом маршруту 2. При об'єднанні маршрутів 1 і 2 дотримуємося таких умов:
- послідовність розташування пунктів на маршруті 1 від початку і до пункту i * не змінюється;
- пункт i * зв'язується з пунктом j *;
- послідовність розташування пунктів на маршруті 2 від пункту j * і до кінця не змінюється.
Повторюємо кроки 1-4 до тих пір, поки при черговому повторенні не вдасться знайти Smax, який задовольняє трьом умовам з кроку 1.
Розраховуємо сумарний пробіг автотранспорту.
ОПИС ПОСЛІДОВНОГО РІШЕННЯ МЕТОДОМ КЛАРКА_РАЙТА.
Весь хід послідовного вирішення задачі представлений в таблиці 4.
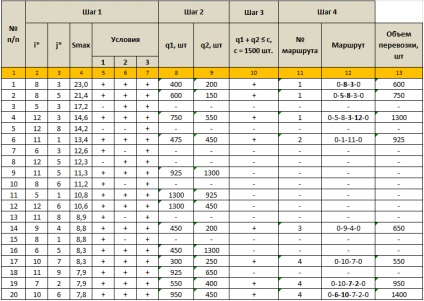
Таблиця 4. Ходи і проміжні результати виконання завдання
Графа 1 - номер ітерації.
Графа 4 - значення максимального кілометрового виграшу Smax.
Графи 5, 6 і 7 - результати перевірки умов 1, 2 і 3 при виконанні кроку 1. "+" - позитивний результат, "-" - негативний результат.
Графи 8 і 9 - обсяг перевезень за маршрутом 1, до складу якого входить пункт i * (q1), та маршруту 2, до складу якого входить пункт j * (q2).
Графа 10 - перевірка на умова, де c - вантажомісткість транспортного засобу. "+" - позитивний результат перевірки умови, "-" - негативний результат.
Графа 11 - порядковий номер кільцевого маршруту (всього в ході рішення отримано всього чотири кільцевих маршрути, див. Рис. 4).
Графа 12 - структура кільцевого маршруту, що утворився на даній ітерації.
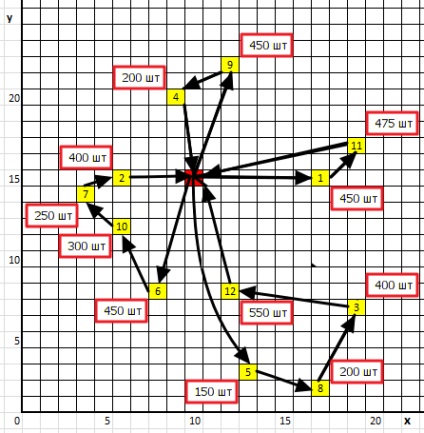
Малюнок 4. Графічне представлення оптимальної схеми доставки
Розглянемо, як відбувається поетапний пошук оптимального рішення задачі. Почнемо з того, що вихідний план розвезення складається з 12 радіальних маршрутів, коли доставка вантажу в кожен з пунктів призначення здійснюється за окремим маршрутом (див. Рис. 2). При цьому загальний пробіг автотранспорту становить (див. Трикутну матрицю відстаней, табл. 3):
L0 = 2 * d01 + 2 * d02 +. + 2 * d012 = 2 * 7.0 + 2 * 4.0 + 2 * 12.4 + 2 * 5.1 +. + 2 * 7.3 = 195 км.
Тепер почнемо покроковий перехід до нового оптимального рішення задачі, яке за рахунок об'єднання радіальних маршрутів в кільцеві дозволить зменшити сумарний пробіг автотранспорту (графічно це нове рішення представлено на рис. 4).
- Об'єднуємо два радіальних маршрути: 0-8-0 (обсяг доставки 200 шт.) І 0-3-0 (обсяг доставки 400 шт.) В загальний кільцевий маршрут (під № 1) 0-8-3-0 (обсяг доставки 600 шт.). При цьому сумарний пробіг автотранспорту скорочується на 23,0 км.
- До кільцевому маршруту № 1 - 0-8-3-0 (600 шт.) Приєднуємо радіальний маршрут 0-5-0 (150 шт.). При цьому пункт 5 приєднуємо до пункту 8. в результаті чого отримуємо нову структуру кільцевого маршруту 0-5-8 -3-0 (750 шт.). Сумарний пробіг автотранспорту скорочується ще на 21,4 км.
- Відзначимо важливість дотримання послідовності пунктів в кільцевому маршруті: саме 0-5-8 -3-0, а не 0-5-3-8-0 або 0-8-3-5-0.
- Якщо i * = 8 і j * = 5, то після об'єднання вони повинні стояти на маршруті один за одним.
- Об'єднання пунктів 3 і 5 забезпечило б виграш в 17,2 км. Але це об'єднання неможливе, оскільки обидва пункти вже входять до складу кільцевого маршруту №1 - 0-5-8-3-0, а об'єднувати можна пункти тільки з різних маршрутів. Таким чином, констатуємо порушення умови 1 і переходимо до наступної ітерації.
- До кільцевому маршруту № 1 - 0-5-8-3-0 (750 шт.) Приєднуємо радіальний маршрут 0-12-0 (150 шт.). При цьому пункт 12 приєднуємо до пункту 3. в результаті чого отримуємо нову структуру кільцевого маршруту 0-5-8-3-12 -0 (1300 шт.). Сумарний пробіг автотранспорту скорочується на 14,6 км.
- Пункти 12 і 8 не об'єднує, оскільки вони вже входять до складу кільцевого маршруту 1 (порушується умова 1).
- Об'єднуємо два радіальних маршрути: 0-1-0 (450 шт.) І 0-11-0 (475 шт.) В загальний кільцевий маршрут (під № 2) 0-11-1-0 (925 шт.). При цьому сумарний пробіг автотранспорту скорочується на 13,4 км.
- Пункти 3 і 6 можна об'єднати через порушення умови 2. Пункт 3 входить до складу кільцевого маршруту 1, і в цьому маршруті він займає «проміжне» становище, тобто він пов'язаний з пунктами 8 і 12: 0-5-8-3- 12-0. Радіальний маршрут 0-6-0 можна було б приєднати до кільцевому маршруту 1 з боку його «крайніх» пунктів - 5 або 12, але до «проміжним» пунктам 3 і 8 його приєднати не можна.
- Повторюють ту ж логіку міркувань, що і в попередніх 7 ітераціях. Відзначимо тільки, що на ітераціях 9, 11, 12, 16 і 18 об'єднання не проводиться тільки через порушення умови
Ітерації з 21 по 60
- Вже не мають сенсу, оскільки їх виконання вже не спричинить за собою зміну плану розвезення.
Сумарний кілометровий виграш за 20 ітерацій становить:
S = 23,0 + 21,4 + 14,6 + 13,4 + 8,8 + 8,3 + 7,9 + 7,8 = 105,3 км
а загальний пробіг автотранспорту, відповідно:
L1 = L0 - S = 195 -105,3 = 89,7 км
Графічно оптимальна схема розвезення представлена на рис. 4. Як видно, оптимальна схема розвезення включає в себе чотири кільцевих маршрути (замість початкових 12 радіальних маршрутів). Сумарний пробіг автотранспорту можна також визначити за такою формулою:
, де Li - довжина i-го маршруту, км; r - кількість маршрутів.
Розглянемо, наприклад, кільцевий маршрут 0-5-8-3-12-0. Протяжність маршруту визначається за формулою (див. Табл. 4):
L1 = d0,12 + d12,3 + d3,8 + d8,5 + d5,0 = 7,3 + 5,1 + 4,1 + 5,4 + 12,0 = 33,9 км.
Аналогічно розраховуємо протяжність інших маршрутів.
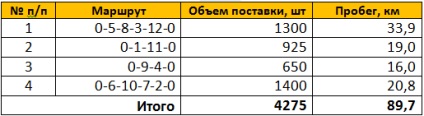
РЕЗУЛЬТАТИ РІШЕННЯ.
Результати рішення задачі зведено в таблицю: