При розгляді кожного питання зустрічаються кількості постійні і змінні.
Постійні колічества.Колічества, що не змінюють своєї величини при розгляді якогось питання, називаються постійними.
Змінні кількості. Кількості, що можуть змінити свою величину, називаються змінними.
Якщо дан коло, то радіус цього кола величина постійна, хорди ж кола, що проходять через якусь точку, що лежить на колі, є величинами змінними.
Точно також зі збільшенням числа сторін правильного описаного багатокутника апофеми їх залишаються величинами постійними, а периметри величинами змінними.
Змінні величини змінюються в якихось межах.
Наближається величина. Коли змінна величина при своїй зміні збільшуючись або зменшуючись наближається до деякої постійної величини так, що різниця між нею і постійною величиною може бути зроблена менше будь-якої даної величини, її називають величиною наближається.
Постійна величина, до якої наближається змінна величина, називається її межею.
Межа. Межею називається така постійна величина, до якої наближається інша змінна величина збільшуючись або зменшуючись, але ніколи її не досягаючи, хоча різниця може бути зроблена менше будь-якої даної величини.
Метод меж. Сукупність властивостей, якими володіють величини наближаються і їх межі, і застосування цих властивостей до вирішення різних питань називають методом меж.
З самого визначення меж випливають такі властивості границі:
Межа є величина постійна.
Наближається величина завжди більш-менш межі.
Різниця між наближається величиною і її межею може бути зроблена менше будь-якої даної величини.
Сума кутів правильного багатокутника, що має n сторін, виражається формулою:
S = 2d (n - 2) = 2nd - 4d
Величина кожного кута буде
Ця величина A є величина змінна. Вона змінюється зі збільшенням n числа сторін правильного багатокутника.
У цьому виразі кількість 2d володіє всіма трьома властивостями межі:
По-перше кількість 2d є величина постійна.
По-друге наближається величина A завжди менше 2d і
нарешті різницю (4d) / n зі збільшенням n може бути зроблена менше будь-якої даної величини.
Зі збільшенням числа сторін правильного багатокутника величина його кожного кута A, збільшуючись все більше і більше, наближається до двох прямим, а два прямих є межа, до якого прагне ця величина.
Якщо в рівнянні X = K + α кількість α може бути зроблено менш всяку даної величини, а K є величина постійна, то X є величина наближається, а K є її межа.
Межа позначають словом lim. (Limite) або попер. (Межа), поставленими перед величиною наближається.
Таким чином пишуть
K = lim X = lim (K + α)
З цього співвідношення видно, що
Нескінченно-мала велічінаесть величина змінна, що має своїм межею нуль.
У методі меж мають значення наступні теореми.
Теорема 129. Якщо дві наближаються величини рівні, то і межі їх рівні.
Дано. Нехай X і Y дві наближаються величини, A і B їх межі, так що
X = A + α, Y = B + β
Змінні величини α і β можуть бути зроблені менш всяку даної величини.
Доведення. З того, що дві наближаються величини X і Y рівні, випливає рівність X = Y або
Тут можуть мати місце такі три припущення:
A> B, A
1. Якби мало місце нерівність A> B, то різниця A - B була б дорівнює деякій кінцевої постійної величини k.
Так як β і α можуть безмежно зменшуватися, то ніяк не можна допустити, щоб різниця β - α дорівнювала постійній кінцевої величиною k, отже, нерівність A> B неможливо.
2. Точно також нерівність A
де l постійна кінцева величина.
З рівності (a) випливає рівність
Це нерівність точно також неможливо, отже, неможливо і припущення A Отже залишається справедливим тільки рівність: A = B (ЧТД). Теорема 130. Ставлення величин наближаються дорівнює відношенню їх меж. Дано дві наближаються величини X = A + α і Y = B + β Потрібно довести, що X / Y = A / B. Доведення. Відношення двох наближаються величин буде Позначимо кінцеву величину цього відносини через l, тоді A + α є наближається величина, що має своїм межею A; Bl + Bβ є наближається величина, що має своїм межею величину Bl. На підставі попередньої теореми рівність (1) веде до рівності Отже, l = A / B звідки (A + α) / (B + β) = A / B (ЧТД). Теорема 131. Зовнішня ламана більше опуклою кривою, що знаходиться всередині ламаної.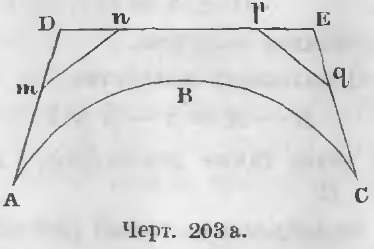
Доведення. Якби крива ABC була менше будь-якої зовнішньої ламаної (рис. 203 а), то існувала б така зовнішня ламана, яка була б менше всякої іншої зовнішньої ламаної, а отже і менше кривої ABC.
Нехай ADEC буде така ламана.
В цьому випадку можна завжди провести так відрізки mn, pq, щоб вони не перетинали кривої ABC, тоді утворюється нова ламана AmnpqC, яка менше ADEC, бо
mn Додавши до цих нерівностей величини Am, np, qC, отримаємо: mn + pq + Am + np + qC Таким чином припущення, що існує зовнішня ламана менше кривої, не має місця. Звідси випливає наслідок. периметр описаного багатокутника більше окружності. Теорема 132. Різниця між периметром однойменного описаного і вписаного багатокутника пріудвоеніі числа сторін може бути зроблена менше будь-якої даної величини. Позначивши через P і p периметри описаного і вписаного багатокутника, що має n сторін (рис. 204), ми знаємо, що (P - p) / p = (OA - Oa) / Oa, (P - p) / p = Aa / Oa, P - p = (Aa / Oa) p (a) Периметр всякого багатокутника більше периметра багатокутника, що полягає всередині, отже, периметр p менше периметра описаного квадрата. Периметр описаного квадрата дорівнює 8 · Oa (8 радіусів), отже, p <8 · Oa. Вставивши замість p до другої частини рівності (a) величину 8 · Oa, ми її збільшимо, отже, P - p <8 · Oa · (Aa/Oa) или При подвоєнні числа сторін довжина відрізка Aa може бути зроблена менше будь-якої даної величини, бо з подвоєнням числа сторін кут AOB, а отже, і кут AOn зменшуються, і похила AO наближається до перпендикуляру nO так, що різниця між непрямої і перпендикуляром може бути зроблена менше всяку даної величини. Теорема 133. Зі збільшенням числа сторін периметри описаного і вписаного багатокутників наближаються до одного і того ж межі. Доведення. з нерівності З подвоєнням числа сторін периметр описаного багатокутника зменшується, а периметр вписаного збільшується. Так як межа Aa дорівнює 0, то межа (P - p) = 0. Звідки попер. P = попер. p, або lim P = lim p (ЧТД). Теорема 134. Коло є межа периметрів багатокутників вписаних і описаних. При подвоєнні числа сторін периметр правильного описаного багатокутника зменшується, а периметр вписаного збільшується. При цьому периметр описаного багатокутника більше, а вписаного менше окружності. Так як різниця між периметрами описаного і вписаного багатокутників може бути зроблена менше будь-якої даної величини, то і поготів з поступовим подвоєнням числа сторін різниця між периметрами правильних багатокутників описаних і окружністю, а також між колом і периметрами вписаних правильних багатокутників може бути зроблена менше будь-якої даної величини , отже: Окружність є межа периметрів вписаних і описаних багатокутників. Теорема 135. Кола пропорційні радіусів. Доведення. Позначимо довжини двох кіл через O і O ', їх радіуси через R і R'. Впишемо в обидві окружності правильні багатокутники, що мають n сторін. Позначивши їх периметри через Pn і Pn ', ми маємо рівність то попереднє рівність дає З послідовним збільшенням числа сторін різниці α і β між колами і периметрами вписаних багатокутників можуть бути зроблені менше всякої даної величини, отже, різниці O - α, O '- β є величинами, що наближаються, а величини O і O' їх межі. На підставі теореми 130 маємо рівність (O - α) / (O '- β) = O / O', звідки На підставі рівності O / R = O '/ R' або O / 2R = O '/ 2R' випливає наслідок. ставлення кожного кола до свого діаметру є величина постійна. Це постійне відношення кола до діаметру називають буквою π. Довжина окружностіравна радіусу, помноженому на 2π. Тут довжина виражається в тих же одиницях, в яких виражається радіус. Абстрактне кількість π є величина несумірна. Наближена величина його 22/7 дана Архімедом. Вона висловлює щиру величину π з точністю до 0,01. Мецій, що жив в кінці 16-го століття, знайшов для π наближену величину 355/113 = 3,141592 з точністю до 0,000001. Це відношення легко пам'ятати, якщо його подати у вигляді Довжина дуги, що має n градусів. Окружність має 360 °. Довжина кола радіуса R виражається формулою 2πR. Довжина одного градуса буде величина (2πR) / 360. Позначивши через s довжину дуги, що має n градусів, маємо: Формула (a) пов'язує три величини: n число градусів дуги, s її довжину і R радіус кола. Вона дає можливість визначити одну з них по двох інших. Формула, що виражає довжину окружності, приймає для R = 1 вид звідки видно, що 2π висловлює довжину окружності, описаної радіусом рівним одиниці. Для визначення π обчислюють периметри правильних багатокутників вписаного і описаного з однаковим числом сторін. Довжина кола укладається між периметрами цих багатокутників. Вона менше периметрів описаних і більше периметрів вписаних багатокутників. Різниця між периметрами вкаже в яких межах полягає похибка у визначенні кола, а отже і у визначенні π. Щоб зменшити цю похибку у визначенні π, послідовно обчислюють периметри багатокутників з подвоєним числом сторін. Різниця між периметрами їх буде все менше і менше, а отже, збільшується і точність, з якою можна визначити π. Позначивши довжину сторони правильних багатокутників, що мають n сторін, вписаного через an. описаного через An і радіусу через r, ми для визначення довжини сторони вписаного багатокутника з подвоєним числом сторін користується формулою: а для визначення сторони описаного багатокутника по стороні вписаного формулою: Позначивши через Pn і pn периметри описаного і вписаного правильного багатокутника, маємо: Наближена величина π задовольняє нерівності: в яких an і An обчислені для окружності з радіусом рівним 1, отже, в формулах, їх визначають приймають r = 1. Формули (1) і (2) для r = 1 приймають вид: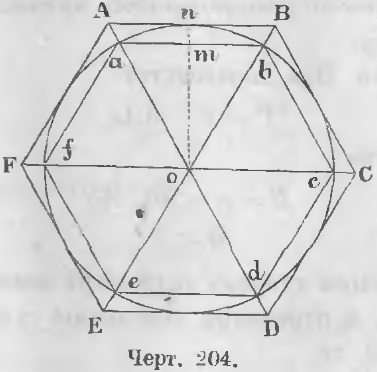
P - p <8AaВизначення величини π
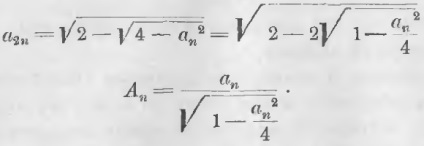
Припустивши, що n = 6, ми для a6 боку правильного вписаного шестикутника при r = 1 маємо:

Помноживши ці величини на число сторін, маємо наступну таблицю периметрів правильних вписаних і описаних багатокутників відповідного числа сторін, обчислених з точністю до 6 десяткових знаків

З цієї таблиці видно, що різниця між периметрами правильних багатокутників вписаного і описаного все зменшується.
Для 96-кутника вона вже менше 0,01, а для багатокутника, що має 3072 боку, вона менше 0,00001.
Архімед зупинився на обчисленні боку 96-кутника і дав наближену величину π з точністю до 0,01. Мецій дав для π величину π = 355/113 = 3,1415920 з точністю до 0,000001.