Суть прийому полягає в наближенні підінтегральної функції на відрізку [a, b] інтерполяційним многочленом другого ступеня. тобто наближення графіка функції на відрізку параболою.
Формулою Сімпсона (див. Рисунок 1.5) називається інтеграл від інтерполяційного многочлена другого ступеня на відрізку [a, b]:
де. і - значення функції у відповідних точках (на кінцях відрізка і в його середині).
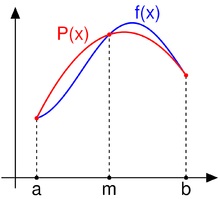
Малюнок 1.5 - Метод парабол для інтервалу ...
[A, b] без розбивки
На відміну від методів прямокутників і трапецій в даному випадку підінтегральна функція апроксимується поліномом другого ступеня () не на одному, а на двох сусідніх ділянках (рисунок 1.6). Тому кількість ділянок, на які розбивається відрізок. має бути парним.
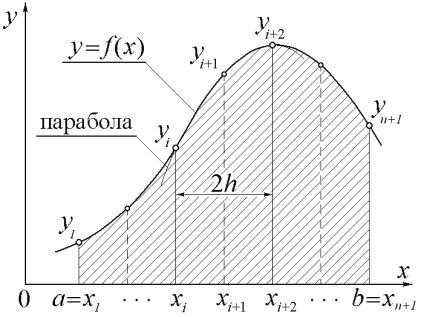
Малюнок 1.6 - Метод Сімпсона при розбитті інтервалу інтегрування рівномірної сіткою
Похибка обчислення певного інтеграла з використанням методу Сімпсона (методу парабол) можна оцінити за формулою:
де - максимальне значення модуля четвертої похідної на ділянці. тобто складова формула Сімпсона істотно точніше, ніж формули прямокутників і трапецій. Вона має на відрізку [а, b] четвертий порядок точності (Rn = 0 (h 4)).
З виразів похибок видно, що формули середніх прямокутників і трапецій точні для многочленів першого ступеня, тобто для лінійних функцій, а формула Сімпсона точна для многочленів до третього ступеня (для них похибка дорівнює нулю).
В інженерній практиці формули оцінки похибки не використовується так як вимагає рішення додаткової завдання пошуку максимуму вищих похідних підінтегральної функції. Більш зручним методом оцінки похибки обчислень певного інтеграла є метод базується на правилі Рунге (правило подвійного рахунку). Певний інтеграл обчислюється двічі: один раз з кроком інтегрування. а інший раз - з меншим кроком інтегрування h2 = h1 / 2. Співвідношення правила Рунге, справедливе для всіх способів наближеного обчислення інтеграла
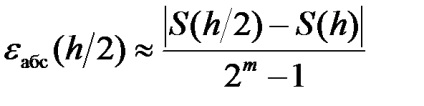
де S (h / 2) і S (h) - наближені значення інтеграла, обчислені при кроках розбиття відрізка [a. b], що відрізняються один від одного в два рази. Для методів середніх прямокутників і трапецій значення m = 2, для методу Сімпсона m = 4. Виходячи з цього, для оцінки похибки обчисленого значення інтеграла з обраним кроком треба повторити обчислення, подвоївши величину кроку, і скористатися наведеними вище співвідношенням. Якщо завдання вимагає отримання результатів з меншою похибкою, ніж була отримана, то необхідно зменшити величину кроку інтегрування вдвічі і повторити обчислення.
Приклад 1. Методами прямокутників, трапецій і Сімпсона обчислити в програмі Excel інтеграл
з кроком інтегрування h = 0.25.
Рішення. Одна з можливих реалізацій формули зазначених методів наведені на малюнках 1.7 (режим відображення формул) і 1.8 (стандартний режим відображення значень в осередках Excel) /
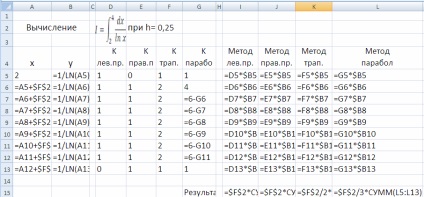
Малюнок 1.7 - Фрагмент листа таблиці Excel обчислення інтеграла
в режимі відображення формул
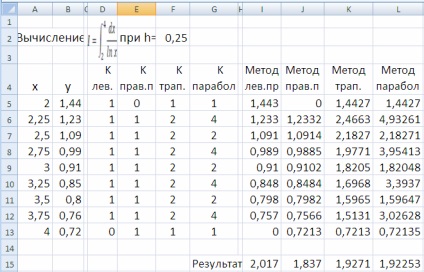
Малюнок 1.8 - Фрагмент листа таблиці Excel обчислення інтеграла в режимі відображення значень в осередках
При розрахунку інтегралів використовувалися такі формули:
- у комірку «В2» вводиться формула «= 1 / LOG (A5)» і за допомогою автозаповнення копіюється в осередку В6-В13;
- у комірку «I5» вводиться формула «= D5 * B5», яка потім копіюється вправо і вниз так, щоб заповнити діапазон I5: L13;
- у комірку «I15» вводиться формула «= $ F $ 2 * СУММ (I5: I13)», яка потім копіюється вправо до комірки «L15»;
- в формулу осередку «K15» додається поділ кроку інтегрування на 2 ( «= $ F $ 2/2 * СУММ (...»), а в осередку «L15» - поділ на 3.
Приклад. Обчислити інтеграл з точністю # 949; = 0,001.
В Excel обчислення інтеграла із заданою точністю, для методів розглянутих вище, можливо тільки із застосуванням методу подвійного рахунку реалізованого в програмі на VBA. Приклад такої програми наведено нижче.
n = 2 'початкове число розбиття
For iter = 1 To 100