1.Чісленние методи інтегрування
2.Вивод формули Сімпсона
4.Вибор кроку інтегрування
1. Чисельні методи інтегрування
Завдання чисельного інтегрування полягає в обчисленні інтеграла
за допомогою ряду значень підінтегральної функції.
Завдання чисельного інтегрування доводиться вирішувати для функцій, заданих таблично, функцією, інтеграли від яких не беруться в елементарних функціях, і т.д. Розглянемо лише функції однієї змінної.
Замість функції, яку потрібно проінтегрувати, проинтегрируем інтерполяційний многочлен. Методи, засновані на заміні підінтегральної функції інтерполяційним многочленом, дозволяють за параметрами многочлена оцінити точність результату або ж по заданій точності підібрати ці параметри.
Чисельні методи умовно можна згрупувати за способом апроксимації підінтегральної функції.
Методи Ньютона-Котеса засновані на апроксимації функції поліномом ступеня. Алгоритм цього класу відрізняється лише ступенем полінома. Як правило, вузли аппроксимирующего полінома - равноотносящіе.
Методи сплайн-інтегрування базуються на апроксимації функції сплайном-КУСКОВО полиномом.
У методах найвищого алгебраїчного точності (метод Гаусса) використовуються спеціально обрані неравноотносящіе вузли, що забезпечують мінімальну похибку інтегрування при заданому (обраному) кількості вузлів.
Методи Монте-Карло використовуються найчастіше при обчисленні кратних інтегралів, вузли вибираються випадковим чином, відповідь носить імовірнісний характер.
Незалежно від обраного методу в процесі чисельного інтегрування необхідно обчислити наближене значення інтеграла і оцінити похибку. Похибка зменшується при збільшенні n-кількості
розбиття відрізка. Однак при цьому зростає похибка округлення
за рахунок підсумовування значень інтегралів, обчислених на часткових відрізках.
Похибка усічення залежить від властивостей підінтегральної функції і довжини часткового відрізка.
2. Висновок формули Сімпсона
Якщо для кожної пари відрізків побудувати многочлен другого ступеня, потім проінтегрувати його і скористатися властивістю адитивності інтеграла, то отримаємо формулу Сімпсона.
Розглянемо підінтегральної функції на відрізку. Замінимо цю підінтегральної функції інтерполяційним многочленом Лагранжа другого ступеня, що збігається з в точках:
і називається формулою Сімпсона.
Отримане для інтеграла значення збігається з площею криволінійної трапеції, обмеженою віссю, прямими, і параболою, що проходить через точки
Оцінимо тепер похибка інтегрування за формулою Сімпсона. Будемо вважати, що у на відрізку існують безперервні похідні. складемо різницю
До кожного з цих двох інтегралів вже можна застосувати теорему про повну загальну середню, оскільки безперервна на і функція невід'ємна на першому інтервалі інтегрування та непозитивним на другому (тобто не змінює знака на кожному з цих інтервалів). Тому:
(Ми скористалися теоремою про повну загальну середню, оскільки - безперервна функція;).
Диференціюючи двічі і застосовуючи потім теорему про повну загальну середню, отримаємо для інший вираз:
З обох оцінок для слід, що формула Сімпсона є точною для многочленів ступеня не вище третьої. Запишемо формулу Сімпсона, напрмер, у вигляді:
Якщо відрізок інтегрування занадто великий, то його розбивають на рівних частин (вважаючи), після чого до кожної пари сусідніх відрізків,. застосовують формулу Сімпсона, саме:
Запишемо формулу Сімпсона в загальному вигляді:
Похибка формули Сімпсона - методу четвертого порядку:
Так як метод Сімпсона дозволяє отримати високу точність, якщо не надто велика. В іншому випадку метод другого порядку може дати більшу точність.
Наприклад, для функції форма трапеції при для дає точний результат, тоді як за формулою Сімпсона отримуємо
3. Геометрична ілюстрація
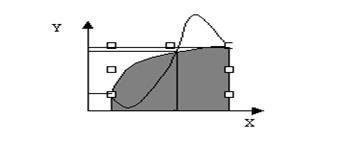
На відрізку довжиною 2h будується парабола, що проходить через три точки,. Площа під параболою, укладена між віссю OX і прямими, приймають рівною інтегралу.
Особливістю застосування формули Сімпсона є той факт, що число розбиття відрізка інтегрування - парне.
Якщо ж кількість відрізків розбиття - непарне, то для перших трьох відрізків слід застосувати формулу, яка використовує параболу третього ступеня, що проходить через чотири перші точки, для апроксимації підінтегральної функції.
Це формула Сімпсона «трьох восьмих».
Для довільного відрізка інтегрування формула (4) може бути «продовжена»; при цьому число часткових відрізків повинна бути кратна трьом (точок).
Можна отримати формули Ньютона-Котеса старших порядків.
- кількість відрізків розбиття;
- ступінь використовуваного полінома;
- похідна -го порядку в точці;
У таблиці 1 виписані коефіцієнти. Кожен рядок відповідає одному набору проміжків вузлами для побудови многочлена k-го ступеня. Щоб скористатися цією схемою для більшої кількості наборів (наприклад, при k = 2 і n = 6), потрібно «продовжити» коефіцієнти, а потім скласти їх.
Алгоритм оцінки похибки формул трапеції і Сімпсона можна записати у вигляді: (7),
де - коефіцієнт, що залежить від методу інтегрування і властивостей підінтегральної функції;
h - крок інтегрування;
p - порядок методу.
Правило Рунге застосовують для обчислення похибки шляхом подвійного прорахунку інтеграла з кроками h і kh.
(8) - апостериорная оцінка. Тоді Iуточн. = + Ro (9), уточнене значення інтеграла.
Якщо порядок методу невідомий, необхідно обчислити I в третій раз з кроком, тобто:
з системи трьох рівнянь:
з невідомими I, А і p отримуємо:
З (10) слід (11)
Таким чином, метод подвійного прорахунку, використаний необхідне число раз, дозволяє обчислити інтеграл із заданим ступенем точності. Вибір необхідного числа розбиття здійснюється автоматично. Можна при цьому використовувати багаторазове звернення до підпрограм відповідних методів інтегрування, не змінюючи алгоритмів цих методів. Однак для методів, які використовують равноотносящіе вузли, вдається модифікувати алгоритми і зменшити вдвічі кількість обчислень підінтегральної функції за рахунок використання інтегральних сум, накопичених при попередніх кратних розбитті інтервалу інтегрування. Два наближених значення інтеграла і, які обчислюють за методом трапеції з кроками і, пов'язані співвідношенням:
Аналогічно, для інтегралів, обчислених за формулою з кроками і, справедливі співвідношення:
4. Вибір кроку інтегрування
Для вибору кроку інтегрування можна скористатися виразом залишкового члена. Візьмемо, наприклад, залишковий член формули Сімпсона:
якщо ê ê , то ê ê .
За заданою точністю e методу інтегрування з останнього нерівності визначаємо відповідний крок.
Однак такий спосіб вимагає оцінки (що на практиці не завжди можливо). Тому користуються іншими прийомами визначення оцінки точності, які по ходу обчислень дозволяють вибрати потрібний крок h.
Розберемо один з таких прийомів. нехай
де - наближене значення інтеграла з кроком. Зменшимо крок в два рази, розбивши відрізок на дві рівні частини і ().
Припустимо тепер, що змінюється не дуже швидко, так що майже постійна:. Тоді і, звідки, тобто.
Звідси можна зробити такий висновок: якщо, тобто якщо,, а - необхідна точність, то крок підходить для обчислення інтеграла з достатньою точністю. Якщо ж, то розрахунок повторюють з кроком і потім порівнюють і і т.д. Це правило називається правилом Рунге.
Однак при застосуванні правила Рунге необхідно враховувати величину похибки обчислень: зі зменшенням абсолютна похибка обчислень інтеграла збільшується (залежність від обернено пропорційна) і при досить малих може виявитися більше похибки методу. Якщо перевищує, то для даного кроку застосовувати правило Рунге не можна і бажана точність не може бути досягнута. У таких випадках необхідно збільшувати значення.
При виведенні правила Рунге ви істотно користувалися припущенням, що. Якщо є тільки таблиця значень, то перевірку «на сталість» можна зробити безпосередньо по таблиці Подальший розвиток наведених алгоритмів дозволяє перейти до адаптивним алгоритмам, в яких за рахунок вибору різного кроку інтегрування в різних частинах відрізка інтегрування в залежності від властивостей зменшується кількість обчислень підінтегральної функції.
Інша схема уточнення значень інтеграла - процес Ейтнена. Проводиться обчислення інтеграла з кроками, причому. Обчислення значень. Тоді (14).
За міру точності методу Сімпсона приймають величину:
Приклад 1. Обчислити інтеграл за формулою Сімпсона, якщо задана таблицею. Оцінити похибку.