Завдання знаходження точного значення певного інтеграла не завжди має рішення. Дійсно, первісну підінтегральної функції в багатьох випадках не вдається представити у вигляді елементарної функції. В цьому випадку ми не можемо точно обчислити визначений інтеграл за формулою Ньютона-Лейбніца. Однак є методи чисельного інтегрування, що дозволяють отримати значення певного інтеграла з необхідним ступенем точності. Одним з таких методів є метод Сімпсона (його ще називають методом парабол).
Навігація по сторінці.
Метод парабол (Сімпсона) - суть методу, формула, оцінка похибки, ілюстрація.
Нехай функція y = f (x) неперервна на відрізку [a; b] і нам потрібно обчислити визначений інтеграл.
Розіб'ємо відрізок [a; b] на n елементарних відрізків довжини точками. Нехай точки є центрами відрізків відповідно. У цьому випадку все "вузли" визначаються з рівності.
Суть методу парабол.
На кожному інтервалі подинтегральная функція наближається квадратичної параболою, що проходить через точки. Звідси і назва методу - метод парабол.
Це робиться для того, щоб в якості наближеного значення визначеного інтеграла взяти, який ми можемо обчислити за формулою Ньютона-Лейбніца. В цьому і полягає суть методу парабол.
Геометрично це виглядає так:
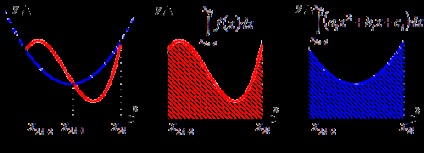
Графічна ілюстрація методу парабол (Сімпсона).
Червоною лінією зображено графік функції y = f (x). синьою лінією показано наближення графіка функції y = f (x) квадратичними параболами на кожному елементарному відрізку розбиття.
Висновок формули методу Сімпсона (парабол).
В силу п'ятого властивості визначеного інтеграла маємо.
Для отримання формули методу парабол (Сімпсона) нам залишилося обчислити.
Нехай (ми завжди можемо до цього прийти, провівши відповідне геометричне перетворення зсуву для будь-якого i = 1, 2. n).
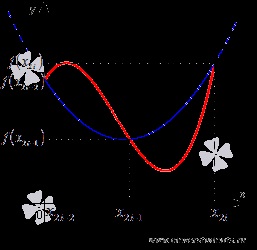
Покажемо, що через точки проходить лише одна квадратична парабола. Іншими словами, доведемо, що коефіцієнти визначаються єдиним чином.
Так як - точки параболи, то справедливо кожне з рівнянь системи
Записана система рівнянь є система лінійних алгебраїчних рівнянь щодо невідомих змінних. Визначником основної матриці цієї системи рівнянь є визначник Вандермонда, а він відмінний від нуля для незбіжних точок. Це вказує на те, що система рівнянь має єдине рішення (про це йдеться в статті рішення систем лінійних алгебраїчних рівнянь), тобто, коефіцієнти визначаються єдиним чином, і через точки проходить єдина квадратична парабола.
Перейдемо до знаходження інтеграла.
Використовуємо ці рівності, щоб здійснити останній перехід в наступному ланцюжку рівностей:

Таким чином, можна отримати формулу методу парабол:

Формула методу Сімпсона (парабол) має вигляд
.
Оцінка абсолютної похибки методу Сімпсона.
Абсолютна похибка методу Сімпсона оцінюється як.
Приклади наближеного обчислення визначених інтегралів методом Сімпсона (парабол).
Розберемо застосування методу Сімпсона (парабол) при наближеному обчисленні визначених інтегралів.
Зазвичай зустрічається два типи завдань:
- У першому випадку потрібно наближено обчислити визначений інтеграл за формулою Сімпсона для заданого n.
- У другому випадку просять знайти наближене значення певного інтеграла методом Сімпсона (парабол) з точністю (наприклад, з точністю до однієї тисячної).
Виникає логічне запитання: "З яким ступенем точності проводити проміжні обчислення"?
Відповідь проста - точність проміжних обчислень повинна бути достатньою. Проміжні обчислення слід проводити з точністю на 3-4 порядки вище, ніж порядок. Також точність проміжних обчислень залежить від числа n - чим більше n. тим точніше слід проводити проміжні обчислення.
Обчисліть певний інтеграл методом Симпсона, розбивши відрізок інтегрування на 5 частин.
З умови ми знаємо, що a = 0; b = 5; n = 5; .
Формула методу Сімпсона (парабол) має вигляд. Для її застосування нам потрібно обчислити крок, визначити вузли і обчислити відповідні значення підінтегральної функції.
Проміжні обчислення будемо проводити з точністю до чотирьох знаків (округляти на п'ятому знаку).
Отже, обчислюємо крок.
Переходимо до вузлів і значенням функції в них:
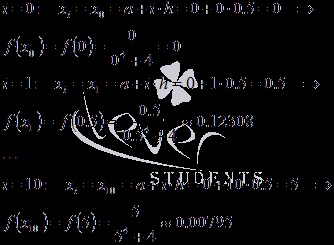
Для наочності і зручності результати зведемо в таблицю:
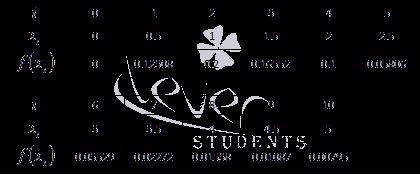
Підставляємо отримані результати в формулу методу парабол:

Ми спеціально взяли певний інтеграл, який можна обчислити за формулою Ньютона-Лейбніца, щоб порівняти результати.
Результати збігаються з точністю до сотих.
Обчисліть певний інтеграл методом Симпсона з точністю до 0.001.
У нашому прикладі a = 0..
Насамперед нам потрібно визначити n. Для цього звернемося до нерівності для оцінки абсолютної похибки методу Сімпсона. Можна сказати, що якщо ми знайдемо n. для якого буде виконуватися нерівність, то при використанні методу парабол для обчислення вихідного інтеграла абсолютна похибка не перевищить 0.001. Остання нерівність можна переписати у вигляді.
З'ясуємо, яке найбільше значення приймає модуль четвертої похідної підінтегральної функції на відрізку інтегрування.

Область значень функції є інтервал, а відрізок інтегрування містить точки екстремуму, тому.
Підставляємо знайдене значення в нерівність і вирішимо його:
Так як n є натуральним числом (це ж кількість відрізків, на які розбивається відрізок інтегрування), то можна брати n = 10, 11, 12, ... Щоб не робити зайвих обчислень, візьмемо n = 10.
Тепер діємо як в попередньому прикладі. У проміжних обчисленнях округлення будемо проводити на шостому порядку.
Знаходимо вузли і значення підінтегральної функції в них:
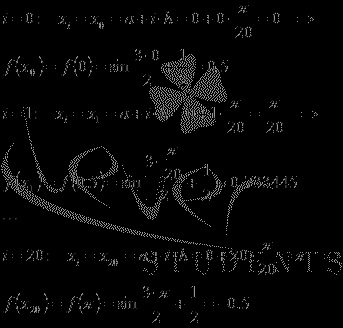
Результати обчислень об'єднуємо в таблицю:

Підставляємо значення в формулу методу парабол:

Таким чином, за методом Сімпсона отримано наближене значення певного інтеграла з точністю до 0.001.
Дійсно, обчисливши вихідний інтеграл за формулою Ньютона-Лейбніца, отримуємо
Знаходження в багатьох випадках важко. Можна обійтися без цього, застосувавши альтернативний підхід до використання методу парабол. Його принцип описаний в розділі метод трапецій. так що не будемо повторюватися.
Який же метод застосовувати при чисельному інтегруванні?
Точність методу Сімпсона (парабол) вище точності методу прямокутників і трапецій для заданого n (це видно з оцінки абсолютної похибки), так що його використання переважніше.
Слід пам'ятати про вплив обчислювальної похибки на результат при великих n. що може віддалити наближене значення від точного.