Доброго дня шановні радіоаматори!
Вітаю вас на сайті "Радіоаматор"
Системи числення застосовуються при створенні програм для мікроконтролерів
Хочеться нам, чи ні, шановні читачі, але осягаючи ази програмування мікроконтролерів, нам доведеться трохи розворушити своє «сіра речовина», повернути на місце «кульки», які іноді заходять за «ролики», змастити їх (можна снікерси) і заштовхати в свою безрозмірну пам'ять (але не занадто глибоко) деякі нові знання, без яких не обійтися.
Отже, системи числення, що це таке і навіщо нам це потрібно знати.

Система числення - символічний метод запису чисел, подання чисел за допомогою письмових знаків (думаємо «Один», а записуємо «1»).
Хоча буває, особливо у людей з загребущими лапами, що думають «Один", а записують «О». В середньому, звичайний росіянин знайомий з двома такими системами, а користується у своїй щоденній практиці тільки однієї (більше і не треба). Ми всі знаємо римську систему числення під назвою - "римські цифри" (ще зі шкільної пори) і, рідну і близьку нам, - десяткову систему числення.
Чому ми раптом заговорили про «циферки»? Справа в тому, що як ви напевно вже й самі здогадалися з попередніх статей, мікроконтролер не розуміє звичні нам набори цифр (згадуйте - все команди для нього складаються з набору тільки двох цифр: нуля і одиниці), а спілкуватися з ним треба.
Для спілкування з мікро контролером (та й взагалі з усією мікропроцесорної, цифровою технікою) існує двійкова система числення. У двійковій системі числення все числа записуються тільки двома символами - «0» і «1». Чому для цифрової техніки обрана саме двійкова система числення. А справа в тому, що своїх «мізків» у цифровій техніці немає, і розпізнають вони цифри не очима, а рівнями напруги на своїх входах. Для розпізнавання «0» і «1» досить двох рівнів напруги (а якби користувалися десятковою системою числення, то знадобилося б уже десять рівнів напруги).
Прийнято вважати, що:
- цифрі «1» відповідає високий рівень напруги
- цифрі «0» відповідає низький рівень напруги.
Наприклад, якщо на «ніжку» мікроконтролера (при напрузі його живлення рівному 5 вольт) подати 5 вольт, то він зрозуміє, що це «1», а якщо нічого не подати, а замкнути «ніжку» на «землю», то він зрозуміє, що це «0». Також і в зворотному порядку. Якщо мікроконтролер повинен передати «1» то він виставляє на своїй «ніжці» висока напруга - 5 вольт, а якщо «0» - то низька напруга - 0 вольт. Тобто, розпізнання цифр 0 і 1 в цифровій техніці відбувається двома рівнями сигналу.
Цікаво, що висновок мікроконтролера може мати ще й третій стан - і не «0», і не «1», а так зване «Z- стан». Тобто, на «ніжці» і не «висока», і не «низьке" напруга. У цьому випадку висновок мікроконтролера вважається відключеним. Фізично, в «Z- стан», висновок звичайно ні від чого не відключається, просто на ньому в цей момент виставляється напруга, яка не відповідає ні низького, ні високої напруги. Справа в тому, що висока напруга, при якому мікроконтролер однозначно визначає, що це «1», не відповідає строго 5 вольт, а може перебувати в деякому проміжку: від 2,5 до 5 вольт. А низька напруга, при якому мікроконтролер однозначно визначає, що це «0», не повинно бути вище 0,5 вольт. Якщо напруга на «ніжці" мікроконтролера буде більше 0,5 вольт, але менше ніж 2,5 вольт, то мікроконтролер не зможе розпізнати «0» це, або «1». Це і є третій стан «Z - стан» - напруга на «ніжці» начебто є, але мікроконтролер на нього ніяк не реагує.
У цифровій техніці високий рівень напруги, відповідний «1», називають - логічна одиниця. а низький рівень напруги, відповідний «0», називають логічним нулем.
Давайте подивимося, як числа десяткової системи відповідають числам в двійковій системі:
1 - 1
2 - 10
3 - 11
5 - 101
10 - 1010
200 - 11001000
Перевести число з десяткової системи в двійкову і назад, дуже просто. Досить мати калькулятор з інженерними функціями, або скористатися стандартним калькулятором «Windows», перевівши його в «інженерний режим»:
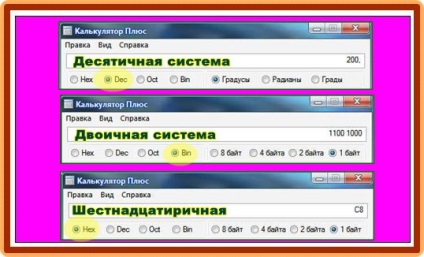
Щоб не плутати числа десяткової системи з числами двійкової системи, в останніх, в кінці числа дописують символ: «В»
200 - 11001000В
У мовах програмування такі символи додають в початок числа.
200 - 0b11001000. або
200 - # b11001000
Десяткові числа в мовах програмування записуються як зазвичай, без всяких додавань. Але а в не "мови програмування», до них може дописуватися буква «D»:
200D - 0b11001000
І ще, якщо користуючись числами в десятковій системі, ми говоримо, наприклад «п'ять», то в двійковій системі ми повинні говорити не «сто один», а «один-нуль-один».
Арифметичні операції в двійковій системі числення. У двійковій системі з числами можна витворяти те ж саме, що і в десяткового:
- складати
- вичитати
- множити
- ділити
Природно, що для виконання арифметичних операцій над двійковими числами ми з успіхом можемо скористатися і калькулятором, але знати, як це робиться ручкою на папері - корисно, стане в нагоді. Ми розглянемо для прикладу тільки дві операції - додавання і множення. Вони простіше для розуміння, а в подальшому, якщо буде потрібно то розглянемо і інші операції (але ви можете це зробити і самостійно).
Додавання.
Додавання проводиться в стовпчик також як і з десятковими числами.
Правила, які треба дотримуватися при складанні:
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 10 - в цьому випадку процес складання відбувається так само як, наприклад, і при додаванні 5 + 5 в десятковій системі - «п'ять плюс п'ять одно десять, нуль пишемо, один« на розум »пішло» Те, що пішло « на розум », потім ми переносимо в наступний розряд.
Для двійкової системи: «один плюс один дорівнює один-нуль, нуль пишемо, один« на розум »пішло».
Для прикладу:
- в десяткової: 5 + 5 = 10
- в двійковій: 101 + 101 = 1010. а тепер в стовпчик:
101
+
101
Починаємо справа-наліво (як завжди):
1 + 1 = 10. 0 пишемо, 1 на «розум пішло» (... .0)
0 + 0 = 0 + 1 з «розуму беремо» = 1 (... .10)
1 + 1 = 10 так і пишемо 10 (1010)
і отримуємо результат: 1010, що дорівнює 10 в десятковій системі.
Множення.
Правила, які треба дотримуватися при множенні:
0х0 = 0
0х1 = 0
1х0 = 0
1х1 = 1
На прикладі:
- в десятковій системі:
5х5 = 25
- в двійковій системі:
101х101 = 11001
А тепер в стовпчик (все по звичайним законам математики):
101
х
101 ---
101 - множимо 1 на 101
000 - множимо 0 на 101
101 - множимо 1 на 101
---
11001
- все рядки складаємо, і отримуємо результат 25.
Цікаво, що при програмуванні в мікроконтролері операції множення (не всі мікроконтролери можуть самостійно множити, але все вміють складати і віднімати), результат знаходять не так, як ми це зробили вище, а по іншому - набагато простіше. А як це робиться ми дізнаємося в процесі вивчення команд мікроконтролера.
Крім десяткової і двійковій системи числення, в цифровій техніці застосовується ще одна, третя, система числення - Шістнадцяткова. У шістнадцятковій системі числення все числа позначають не десятьма символами, як в десятковій, і не двома, як в двійковій, а шістнадцятьма: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. Подивимося відповідність чисел шестнадцатиричной системи по відношенню до десяткового і двійковій:
1 - 1 - 1
5 - 101 - 5
10 - 1010 - А
200 - 11001000 - С8
Для позначення шістнадцяткових чисел в кінці дописують латинську букву «Н»:
1Н, 5Н, АН, С8Н
Для запису шістнадцяткових чисел в мовах програмування, їм на початку додають «Ох» або знак «$» (і тут «зелений» відзначився):
С8 = С8Н = ОхС8 = $ С8

Чому в мовах програмування застосовують аж цілих три види систем числення:
- десяткову
- двійкову
- шестнадцатиричную
адже все одно, в ході перекладу програми в машинні коди, вони все прикидаються тільки двійковій системи? В принципі, можна обійтися тільки десятковими цифрами - для нас так буде зручніше, або двійковими - щоб не мучити компілятор перекладом чисел в двійкову систему з інших систем. Але вся справа в тому, що і в системі команд, і інструкціях, які повинен виконувати мікроконтролер, в різних випадках доводиться користуватися числами і в двійковій системі, і в шістнадцятковій. В одних випадках для наочності, а в інших випадках - щоб не ускладнювати собі життя (якщо щось відомо у вигляді числа в шістнадцятковій системі, то навіщо робити зайві рухи тіла і переводити це число в десяткову систему, якщо тільки для наочності). Але смію вас запевнити, що тільки на перших порах ви будете відчувати певний дискомфорт при використанні двійковій і шістнадцятковій систем числення, через короткий час ви вже не будете звертати на це увагу. А може інша система числення вам сподобається настільки, що і в повсякденному житті перейдете на неї. Круто буде, сказати в магазині продавцеві - «Ви мені недодали 3FF рублів». До речі, фанати «нетрадиційної» системи числення, навіть створюють електронний годинник, який показує час в двійковій системі (Скільки час? 1-1-0-0-1-0-1-1).
У наступній статті ми з вами розберемо ще один, більш «темний ліс» - логічні операції. Але а після цього вже перейдемо до вивчення пристрої мікроконтролерів.